Question

Airplanes $ A $ and $ B $ are flying with constant velocity in the same vertical plane at angles $ {30^ \circ } $ and $ {60^ \circ } $ with respect to the horizontal respectively as shown in the figure. The speed of $ A $ is $ 100\sqrt 3 m{s^{ - 1}} $ . At time $ t = 0s $ , an observer in $ A $ finds $ B $ at a distance of $ 500m $ . This observer sees $ B $ moving with a constant velocity perpendicular to the line of motion of $ A $ . If at $ t = {t_0} $ , $ A $ just escapes being hit by $ B $ , $ {t_0} $ in seconds is:

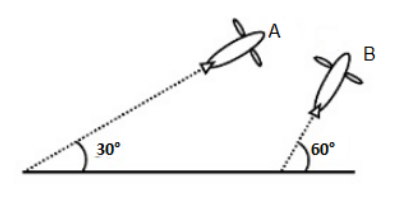
 $ \left( A \right)5 \\
  \left( B \right)7 \\
  \left( C \right)6 \\
  \left( D \right)8 \\ $

Answer 1

Hint :In this question, we are going to first divide the two velocities into horizontal and vertical components. By equating the components, the velocity $ {V_B} $ is calculated. From $ {V_B} $ , the time for the escape can be calculated from the distance given and the vertical component of the velocity $ {V_B} $ .
The horizontal and the vertical components of a velocity $ V $ with projection angle $ \theta $ are $ V\cos \theta $ and $ V\sin \theta $ respectively.
The time taken for $ B $ is
 $ {T_0} = \dfrac{{distance}}{{vertical{\text{ }}component{\text{ }}of speed{\text{ }}of{\text{ }}B}} $

Complete Step By Step Answer:
In the given figure, we can see that the velocities $ {V_A} $ and $ {V_B} $ can be split into its vertical and horizontal components.

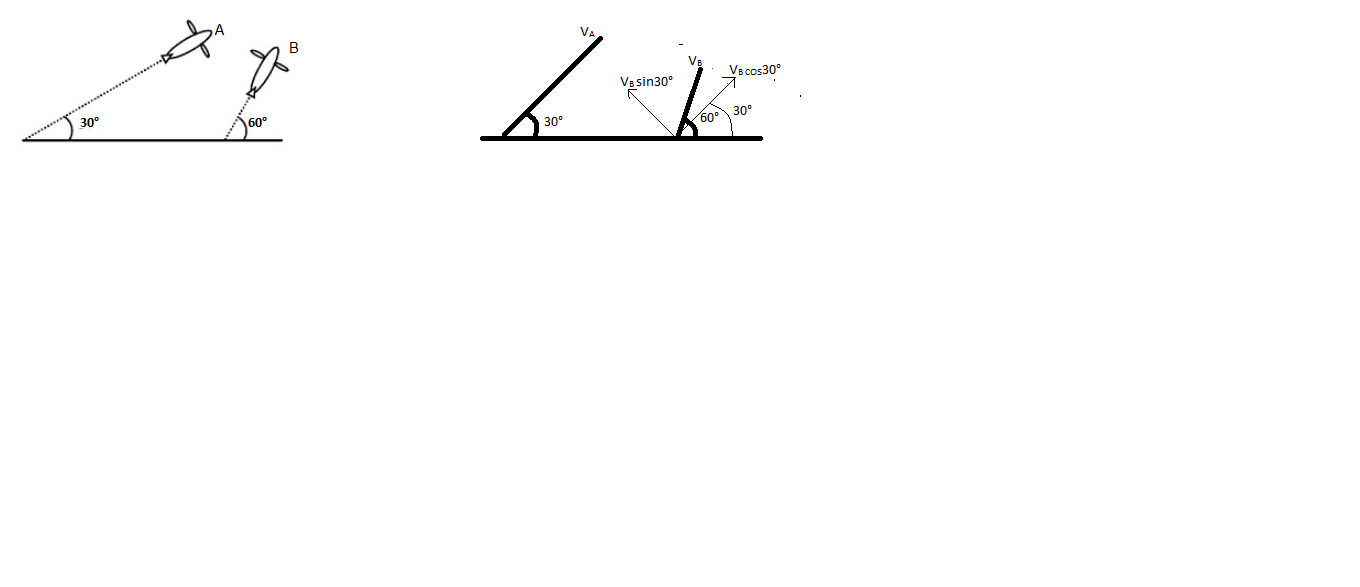
The components of the velocities can be related as
 $ {V_A} = {V_B}\cos {30^ \circ } $
Here, if we put the values of the velocity $ {V_A} $ and $ \cos {30^ \circ } $ , we get, the value of $ {V_B} $ as:
 $ 100\sqrt 3 = {V_B} \times \dfrac{{\sqrt 3 }}{2} $
On solving this, we get
 $ {V_B} = 200m{s^{ - 1}} $
Here, we are given that the distance between the two planes is $ 500m $ and also that the observer sees that the motion of $ B $ moving with a constant velocity perpendicular to the line of motion of $ A $ thus, the time $ t = {t_0} $ at which $ A $ just escapes being hit by $ B $ , is
 $ {T_0} = \dfrac{{distance}}{{vertical{\text{ }}component{\text{ }}of speed{\text{ }}of{\text{ }}B}} $
Putting the values, we get
 $ {T_0} = \dfrac{{500}}{{{V_B}\sin {{30}^ \circ }}} = \dfrac{{500}}{{200 \times \dfrac{1}{2}}} \\
   \Rightarrow {T_0} = 5s \\ $
Hence, option $ \left( A \right)5 $ is the correct answer.

Note :
In the question, we are given that the distance along the line of motion is $ 500m $ , along this direction, the velocity that is prevalent is the vertical component of the velocity along the angle $ {30^ \circ } $ . Where the horizontal component of the velocity $ {V_B} $ is equal to the speed of the airplane $ A $ .