Question

Adjacent sides of a parallelogram are \[11cm\] and \[17cm\] . If the length of one of its diagonals is \[26cm\] , find the length of the other.

Answer 1

Hint: A parallelogram has two diagonals joining two opposite corners. In the given question, we are given the length of one diagonal and have to find the length of the other. We can solve the question by using Apollonius Theorem.

Complete step-by-step answer:
Let us draw a diagram for better understanding:

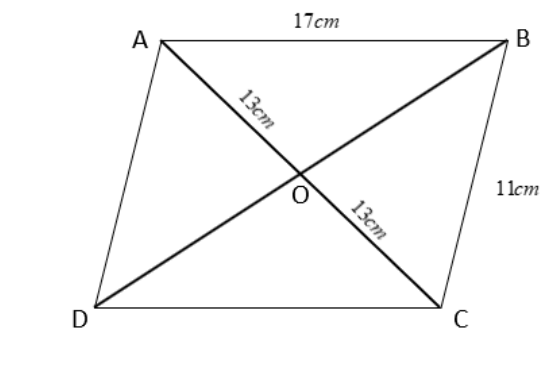
We draw with \[AB = 17cm\] , \[BC = 11cm\] and diagonal \[AC = 26cm\] . We have to find the length of diagonal \[BD\] .
Let the diagonals bisect each other at point \[O\] .
We know that diagonal of a parallelogram bisects each other at a point which divides it into two equal parts.
Hence, we can say that:
 \[AO = OC = \dfrac{1}{2}AC\]
 \[AO = \dfrac{1}{2}(26) = 13cm\]
Similarly, \[BO = OD = \dfrac{1}{2}BD\]
Now in \[\vartriangle ABC\] , \[\overline {BO} \] is the median as it divides \[\overline {AB} \] in two equal parts.
Now to find the length of \[\overline {BO} \] , we can use Apollonius Theorem.
Apollonius Theorem states that “the sum of squares of any of the two sides of a triangle equals to twice its square on half of the third side, along with the twice of its square on the median bisecting the third side”
Using the above theorem, we can conclude that, in \[\vartriangle ABC\] ,
 \[A{B^2} + B{C^2} = 2{(BO)^2} + 2{(AO)^2}\]
Substituting the values by comparing with above formula, we get,
 \[{(17)^2} + {(11)^2} = 2{(BO)^2} + 2{(13)^2}\]
 \[289 + 121 = 2{(BO)^2} + 2(169)\]
 \[289 + 121 = 2{(BO)^2} + 338\]
 \[2{(BO)^2} = 289 + 121 - 338\]
 \[2{(BO)^2} = 72\]
 \[B{O^2} = \dfrac{{72}}{2} = 36\]
Taking square root, we get,
 \[BO = \sqrt {36} \]
 \[BO = 6cm\]
Now to find the length of diagonal \[\overline {BD} \] , we use the following formula:
 \[BD = BO + OD = BO + BO = 2BO\]
 \[BO\] and \[OD\] are equal since \[O\] is a point of intersection of two diagonals.
 \[BD = 2(6)\]
 \[BD = 12cm\]
Hence the length of the other diagonal is \[12cm\] .
So, the correct answer is “ \[12\;cm\] ”.

Note: A simple quadrilateral with two pairs of parallel sides is known as a parallelogram. A parallelogram's opposite or facing sides are of equal length, and the parallelogram's opposite angles are of equal measure.