
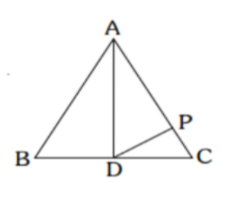
AD is the median of \[\Delta ABC\] and P is a point on AC such that
Area of \[\Delta ADP\] : Area of \[\Delta ABD\] = 2 : 3 and Area of \[\Delta PCD\] : Area of \[\Delta ABC\] = 1 : a. Find the value of a.

Answer
572.1k+ views
Hint: From the given \[\Delta ABC\], AD is the median and P is a point on AC, such that Area of \[\Delta ADP\] : Area of \[\Delta ABD\] = 2 : 3 and Area of \[\Delta PCD\] : Area of \[\Delta ABC\] = 1 : a. By changing the ratios to its fractions, we will get the Area of \[\Delta ADP\] and Area of \[\Delta ABD\]. As AD is the median in the given triangle, it divides the \[\Delta ABC\] into two equal areas. Therefore, Area of\[\Delta ABD\] = Area of \[\Delta ADC\]
Complete step-by-step solution:
We have been given the figure as
We have AD as the median of the \[\Delta ABC\] and P as a point on AC such that we have
Area of \[\Delta ADP\] : Area of \[\Delta ABD\] = 2 : 3 and Area of \[\Delta PCD\] : Area of \[\Delta ABC\] = 1 : a
\[\begin{align}
& \Rightarrow \dfrac{Area(\Delta ADP)}{Area(\Delta ABD)}=\dfrac{2}{3} \\
& \Rightarrow Area(\Delta ADP)=2\text{ and }Area(\Delta ABD)=3 \\
\end{align}\]
We know that AD is the median and divides the \[\Delta ABC\] into two triangles of equal areas.
\[\Rightarrow \] Area of \[\Delta ABD\]= Area of \[\Delta ADC\]
= 3
Now, from the given triangle, we can write that
Area of \[\Delta ADC\] = Area of \[\Delta ADP\]+ Area of \[\Delta DPC\]
\[\Rightarrow \]3 = 2 + Area of \[\Delta DPC\]
Here, we know that from the\[\Delta ABC\]
Area of \[\Delta ABC\] = Area of \[\Delta ABD\]+ Area of \[\Delta ADC\]
\[\Rightarrow \] 3 + 3 = 6
\[\therefore \] Area of \[\Delta ABC\] = 6
Area of \[\Delta PCD\] : Area of \[\Delta ABC\] = 1 : 6
Therefore, the value of a is 6.
Note: We have to know that AD is the median and it divides the triangle into two equal parts. There is another method for the given problem.
Since AD is the median,
Area of \[\Delta ABD\] = Area of \[\Delta ADC\] ………… (1)
Also given that,
\[\Rightarrow \dfrac{Area(\Delta ADP)}{Area(\Delta ABD)}=\dfrac{2}{3}\]
\[\Rightarrow \] Area of \[\Delta ADP\] = \[\dfrac{2}{3}\]\[\times \] Area of \[\Delta ABD\]
Now, we have
Area of \[\Delta ADC\] = Area of \[\Delta ADP\] + Area of \[\Delta DPC\]
From (1) and (2), we get
Area of \[\Delta ABD\] = \[\dfrac{2}{3}\] Area of \[\Delta ABD\] + Area of \[\Delta DPC\]
Area of \[\Delta DPC\] = \[\dfrac{1}{3}\] Area of \[\Delta ABD\]
We know that
Area of \[\Delta ABC\] = 2 \[\times \] Area of \[\Delta ABD\] ……… (4)
Therefore, from (3) and (4), we get
\[\begin{align}
& \dfrac{Area(\Delta PDC)}{Area(\Delta ABC)}=\dfrac{\dfrac{1}{3}Area(\Delta ADB)}{2Area(\Delta ADB)} \\
& \dfrac{Area(\Delta PDC)}{Area(\Delta ABC)}=\dfrac{1}{6} \\
& \\
\end{align}\]
Area of \[\Delta PCD\] : Area of \[\Delta ABC\] = 1 : 6.
Therefore, the value of a is 6.
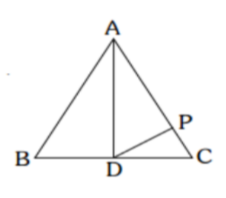
Complete step-by-step solution:
We have been given the figure as

We have AD as the median of the \[\Delta ABC\] and P as a point on AC such that we have
Area of \[\Delta ADP\] : Area of \[\Delta ABD\] = 2 : 3 and Area of \[\Delta PCD\] : Area of \[\Delta ABC\] = 1 : a
\[\begin{align}
& \Rightarrow \dfrac{Area(\Delta ADP)}{Area(\Delta ABD)}=\dfrac{2}{3} \\
& \Rightarrow Area(\Delta ADP)=2\text{ and }Area(\Delta ABD)=3 \\
\end{align}\]
We know that AD is the median and divides the \[\Delta ABC\] into two triangles of equal areas.
\[\Rightarrow \] Area of \[\Delta ABD\]= Area of \[\Delta ADC\]
= 3
Now, from the given triangle, we can write that
Area of \[\Delta ADC\] = Area of \[\Delta ADP\]+ Area of \[\Delta DPC\]
\[\Rightarrow \]3 = 2 + Area of \[\Delta DPC\]
Here, we know that from the\[\Delta ABC\]
Area of \[\Delta ABC\] = Area of \[\Delta ABD\]+ Area of \[\Delta ADC\]
\[\Rightarrow \] 3 + 3 = 6
\[\therefore \] Area of \[\Delta ABC\] = 6
Area of \[\Delta PCD\] : Area of \[\Delta ABC\] = 1 : 6
Therefore, the value of a is 6.
Note: We have to know that AD is the median and it divides the triangle into two equal parts. There is another method for the given problem.
Since AD is the median,
Area of \[\Delta ABD\] = Area of \[\Delta ADC\] ………… (1)
Also given that,
\[\Rightarrow \dfrac{Area(\Delta ADP)}{Area(\Delta ABD)}=\dfrac{2}{3}\]
\[\Rightarrow \] Area of \[\Delta ADP\] = \[\dfrac{2}{3}\]\[\times \] Area of \[\Delta ABD\]
Now, we have
Area of \[\Delta ADC\] = Area of \[\Delta ADP\] + Area of \[\Delta DPC\]
From (1) and (2), we get
Area of \[\Delta ABD\] = \[\dfrac{2}{3}\] Area of \[\Delta ABD\] + Area of \[\Delta DPC\]
Area of \[\Delta DPC\] = \[\dfrac{1}{3}\] Area of \[\Delta ABD\]
We know that
Area of \[\Delta ABC\] = 2 \[\times \] Area of \[\Delta ABD\] ……… (4)
Therefore, from (3) and (4), we get
\[\begin{align}
& \dfrac{Area(\Delta PDC)}{Area(\Delta ABC)}=\dfrac{\dfrac{1}{3}Area(\Delta ADB)}{2Area(\Delta ADB)} \\
& \dfrac{Area(\Delta PDC)}{Area(\Delta ABC)}=\dfrac{1}{6} \\
& \\
\end{align}\]
Area of \[\Delta PCD\] : Area of \[\Delta ABC\] = 1 : 6.
Therefore, the value of a is 6.
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

State and explain Ohms law class 10 physics CBSE

Distinguish between soap and detergent class 10 chemistry CBSE

a Why did Mendel choose pea plants for his experiments class 10 biology CBSE

What is a "free hit" awarded for in limited-overs cricket?

Draw the diagram of the sectional view of the human class 10 biology CBSE




