Question

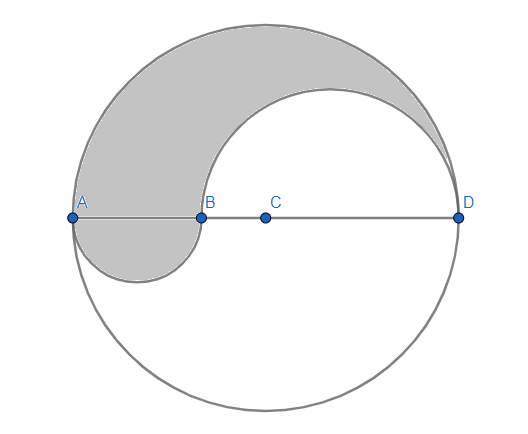
AD is the diameter of a circle of radius 6cm, and AB=BC=CD. Semi-circles are drawn with AB and BD as diameter as shown in the figure. Find the perimeter and area of the shaded region.

Answer 1

Hint: Use the area and perimeter of the semicircle with the radius as AC and subtract or add the other parts to it according to the need to reach the answer.

Complete step-by-step answer:
In the question, it is given in the question that AB=BC=CD, and also we know AD is the diameter and the length of AD is twice the radius i.e., 12cm.
Therefore AB=BC=CD= $\dfrac{1}{3}\times AD=4cm$ .
Now moving to find the perimeter of the shaded region. As we can see in the figure that the perimeter of the shaded region is the length of the semi-circular arc AD added with the length of the semi-circular arc AB and the length of the semi-circular arc BD.
We know that the length of the semicircular arc is $\pi r$ , where r is the radius. Therefore, we get
Perimeter= $\pi \dfrac{\left( AB \right)}{2}+\pi \dfrac{\left( BD \right)}{2}+\pi \dfrac{\left( AD \right)}{2}=\pi \left( 2+4+6 \right)=12\pi \text{ cm}$
Therefore, the perimeter of the shaded region is $12\pi \text{ cm}$ .
Now moving to find the area of the shaded region. As we can see in the figure, the area of the shaded region is the area of semi-circular part AD minus the area of semi-circular part BD plus the area of semi-circular part AB.
We know that the area of the semicircular arc is $\dfrac{\pi {{r}^{2}}}{2}$ , where r is the radius. Therefore, we get
Area= \[\dfrac{\pi }{2}{{\left( \dfrac{AB}{2} \right)}^{2}}-\dfrac{\pi }{2}{{\left( \dfrac{BD}{2} \right)}^{2}}+\dfrac{\pi }{2}{{\left( \dfrac{AD}{2} \right)}^{2}}\]
Area= \[\dfrac{\pi }{2}\left( {{2}^{2}}-{{4}^{2}}+{{6}^{2}} \right)=\dfrac{\pi }{2}\left( 4-16+36 \right)=\dfrac{\pi }{2}\times 24=12\pi \text{ c}{{\text{m}}^{2}}\]
Therefore, the area of the shaded region is $12\pi \text{ c}{{\text{m}}^{2}}$.

Note: It is prescribed to learn all the basic theorems related to circles as they are regularly used in the questions related to circles and triangles, as we did in the above question. Also, learn all the formulas related to the area and perimeter of the circle.