Question

AD is an altitude of an equilateral \[\Delta ABC\] . On AD as base, another equilateral \[\Delta ADE\] is constructed. Prove that:
\[\dfrac{ar\left( \Delta ADE \right)}{ar\left( \Delta ABC \right)}=\dfrac{3}{4}\]

Answer 1

Hint: Assume that each side of the equilateral \[\Delta ABC\] is x units. Use the formula, \[Area=\dfrac{\sqrt{3}}{4}{{\left( side \right)}^{2}}\] and calculate the area of \[\Delta ABC\] . We know that the length of the perpendicular of an equilateral triangle is \[\dfrac{\sqrt{3}}{2}side\] . Now, get the length of the perpendicular of \[\Delta ABC\] . It is given that the length of the base of \[\Delta ADE\] is equal to the length of the perpendicular of \[\Delta ABC\] . So, the length of each side of \[\Delta ADE\] is equal to the length of the perpendicular of \[\Delta ABC\] . Now, use the formula, \[Area=\dfrac{\sqrt{3}}{4}{{\left( side \right)}^{2}}\] and calculate the area of \[\Delta ADE\] . Then, calculate \[\dfrac{ar\left( \Delta ADE \right)}{ar\left( \Delta ABC \right)}\].

Complete step-by-step answer:
First of all, let us assume that each side of the equilateral \[\Delta ABC\] is x units.
The length of each side of \[\Delta ABC\] = x ………………………………..(1)

We know the formula of area of equilateral triangle, \[Area=\dfrac{\sqrt{3}}{4}{{\left( side \right)}^{2}}\] ………………………………..(2)
From equation (1), we have the length of each side of \[\Delta ABC\] .
Now, putting the value of length of each side equal to x in equation (2), we get
The area of \[\Delta ABC\] = \[\dfrac{\sqrt{3}}{4}{{\left( x \right)}^{2}}=\dfrac{\sqrt{3}{{x}^{2}}}{4}\] …………………………….(3)
We know that the length of the perpendicular of an equilateral triangle is \[\dfrac{\sqrt{3}}{2}side\] .
Since the side if \[\Delta ABC\] is x units so, the length of the perpendicular of \[\Delta ABC\] is \[\dfrac{\sqrt{3}}{2}x\] ………………………………(4)
It is given that the length of the base of \[\Delta ADE\] is equal to the length of the perpendicular of \[\Delta ABC\] .
From equation (4), we have the length of the perpendicular of \[\Delta ABC\] .
The length of the base of \[\Delta ADE\] = \[\dfrac{\sqrt{3}}{2}x\] ……………………………………(5)
As \[\Delta ADE\] is an equilateral triangle so, the length of each side is same as the length of the base of \[\Delta ADE\] .
The length of each side of \[\Delta ADE\] = \[\dfrac{\sqrt{3}}{2}x\] ………………………………….(6)
From equation (6), we have the length of each side of \[\Delta ADE\] .
Now, putting the value of length of each side equal to x in equation (2), we get
The area of \[\Delta ADE\] = \[\dfrac{\sqrt{3}}{4}{{\left( \dfrac{\sqrt{3}}{2}x \right)}^{2}}=\dfrac{3}{4}\times \dfrac{\sqrt{3}{{x}^{2}}}{4}\] …………………………….(7)
Now, from equation (3) and equation (7), we have the area of \[\Delta ABC\] and \[\Delta ADE\] .
\[\dfrac{ar\left( \Delta ADE \right)}{ar\left( \Delta ABC \right)}=\dfrac{\dfrac{3}{4}\times \dfrac{\sqrt{3}{{x}^{2}}}{4}}{\dfrac{\sqrt{3}{{x}^{2}}}{4}}=\dfrac{3}{4}\]
LHS = RHS.
Hence, proved.

Note: While solving this question, one might get confused and can think why the length of the perpendicular of an equilateral triangle is \[\dfrac{\sqrt{3}}{2}side\] .
Let us assume an equilateral triangle whose length of each side is x units.

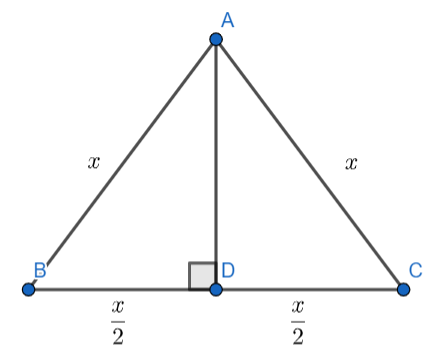
In the \[\Delta ABC\] , AD is perpendicular to the base BC.
We know the property that the perpendicular bisects the base in an equilateral triangle.
So, the perpendicular AD bisects the base BC,
Therefore, \[BD=CD\] …………………………….(1)
Since the length of each side of \[\Delta ABC\] is equal to x so, the length of the base BC is also x.
BC = x …………………………………(2)
From the figure, we can see that
\[\Rightarrow BC=BD+CD\]
Now, from equation (1) and equation (2), we get
\[\begin{align}
  & \Rightarrow x=BD+BD \\
 & \Rightarrow x=2BD \\
\end{align}\]
\[\Rightarrow \dfrac{x}{2}=BD\] …………………………………(3)
Now, in \[\Delta ADB\] , we have
\[\angle ADB=90{}^\circ \] …………………………………(4)
Hypotenuse = AB = x (side of each side of \[\Delta ABC\] is equal to x) …………………………………(5)
Base = BD = \[\dfrac{x}{2}\] ……………………………….(6)
Perpendicular = AD ………………………………….(7)
Since \[\Delta ADB\] is an equilateral triangle, so we can apply the Pythagoras theorem here.
\[{{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\] ………………………..(8)
Now, from equation (4), equation (5), equation (6), equation (7), and equation (8), we get
\[\begin{align}
  & \Rightarrow {{\left( x \right)}^{2}}={{\left( AD \right)}^{2}}+{{\left( \dfrac{x}{2} \right)}^{2}} \\
 & \Rightarrow {{x}^{2}}=A{{D}^{2}}+\dfrac{{{x}^{2}}}{4} \\
 & \Rightarrow {{x}^{2}}-\dfrac{{{x}^{2}}}{4}=A{{D}^{2}} \\
 & \Rightarrow \dfrac{4{{x}^{2}}-{{x}^{2}}}{4}=A{{D}^{2}} \\
 & \Rightarrow \dfrac{3{{x}^{2}}}{4}=A{{D}^{2}} \\
\end{align}\]
\[\Rightarrow \dfrac{\sqrt{3}x}{2}=AD\]
Here, AD is the length of the perpendicular and x is the length of the side of equilateral \[\Delta ABC\] .
Therefore, the length of the perpendicular of an equilateral triangle is \[\dfrac{\sqrt{3}}{2}side\] .