Question

AD bisects angle \[A\] of triangle\[ABC\], where \[D\] lies on \[BC\] and angle \[C\] is greater than angle \[B\], then show that the angle \[ADB\] is greater than angle \[ADC.\]

Answer 1

Hint: At first we will try to find out the value of the angles of the triangle \[ADB\] and triangle \[ADC\]in terms of angles\[A,B\& C\]. Then we will find the relation between the required angles.

Complete step-by-step answer:
It is given that, \[AD\] bisects angle \[A\] of triangle\[ABC\], where \[D\]lies on \[BC\] and angle \[C\] is greater than angle\[B\].

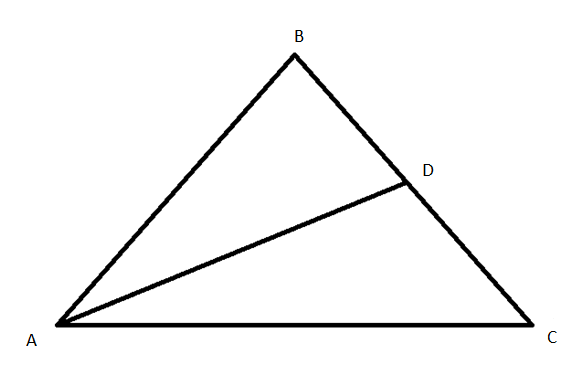
We know that sum of the all the angles of triangle is \[{180^ \circ }.\]
Since, \[AD\] bisects angle \[A\] of triangle\[ABC\],
We can write \[\angle DAB = \dfrac{1}{2}\angle A\]
So, now let us consider the triangle \[ADB\] in that since we have,
Sum of all the angles is \[{180^ \circ }.\]
That is the sum of the angles in the triangle\[ABC\] ,
\[\angle ABD + \angle ADB + \angle BAD = {180^ \circ }.\]
We know that\[\angle BAD = \dfrac{1}{2}\angle A\] and \[\angle ABD = \angle B\]on substituting the known values we get,
\[\angle ADB = {180^ \circ } - \angle B - \dfrac{1}{2}\angle A\]
Similarly, from the triangle \[ADC\] using the fact that Sum of all the angles is \[{180^ \circ }.\]we have,
\[\angle ACD + \angle ADC + \angle CAD = {180^ \circ }.\]
Here we know that \[\angle CAD = \dfrac{1}{2}\angle A\] and \[\angle ACD = \angle C\] on substituting the values in the above equation we get,
\[\angle ADC = {180^ \circ } - \angle C - \dfrac{1}{2}\angle A\]
It is also given that,\[\angle C > \angle B\]
Let us multiply by \[ - 1\]on both sides of the inequality, we get,
\[ - \angle C < - \angle B\]
Now let us add \[{180^ \circ }\] in both sides of the inequality, then we have,
\[{180^ \circ } - \angle C < {180^ \circ } - \angle B\]
Also let us subtract \[\dfrac{1}{2}\angle A\] in both sides of the above inequality then we have,
\[{180^ \circ } - \angle C - \dfrac{1}{2}\angle A < {180^ \circ } - \angle B - \dfrac{1}{2}\angle A\]
We know that from equation (1) and (2) we have \[\angle ADB = {180^ \circ } - \angle B - \dfrac{1}{2}\angle A\] and\[\angle ADC = {180^ \circ } - \angle C - \dfrac{1}{2}\angle A\]
On substituting the values in the inequality we get,
\[\angle ADB > \angle ADC\].

Hence, we have shown that the angle \[ADB\] is greater than angle \[ADC.\]

Note:
Let us consider, \[A > B\] then by multiplying \[ - 1\] with both sides we will have the relation as,\[ - B > - A\] that is the relation greater than is changed to less than and vice versa on multiplying the inequality by \[ - 1\]