Question

What is the acceleration $\overrightarrow a $ at a point P(R,$\theta $) on the circle of radius R for a particle in uniform circular motion? (here ‘v’ is the speed of the particle and $\theta $ is measured from the x-axis)
\[
  {\text{A}}{\text{. }} - \left( {\dfrac{{{{\text{v}}^2}}}{{\text{R}}}\cos \theta } \right)\widehat i + \left( {\dfrac{{{{\text{v}}^2}}}{{\text{R}}}\sin \theta } \right)\widehat j \\
  {\text{B}}{\text{. }} - \left( {\dfrac{{{{\text{v}}^2}}}{{\text{R}}}\sin \theta } \right)\widehat i + \left( {\dfrac{{{{\text{v}}^2}}}{{\text{R}}}\cos \theta } \right)\widehat j \\
  {\text{C}}{\text{. }} - \left( {\dfrac{{{{\text{v}}^2}}}{{\text{R}}}\cos \theta } \right)\widehat i - \left( {\dfrac{{{{\text{v}}^2}}}{{\text{R}}}\sin \theta } \right)\widehat j \\
  {\text{D}}{\text{. }}\left( {\dfrac{{{{\text{v}}^2}}}{{\text{R}}}} \right)\widehat i + \left( {\dfrac{{{{\text{v}}^2}}}{{\text{R}}}} \right)\widehat j \\
 \]

Answer 1

Hint: Here, we will proceed by drawing the figure corresponding to any particle undergoing uniform circular motion. Then, we will show the acceleration acting on the particle at the given point and resolve it into Cartesian components.
Formula Used: ${a_c} = \dfrac{{{{\text{v}}^2}}}{{\text{R}}}$.

Complete Step-by-Step solution:

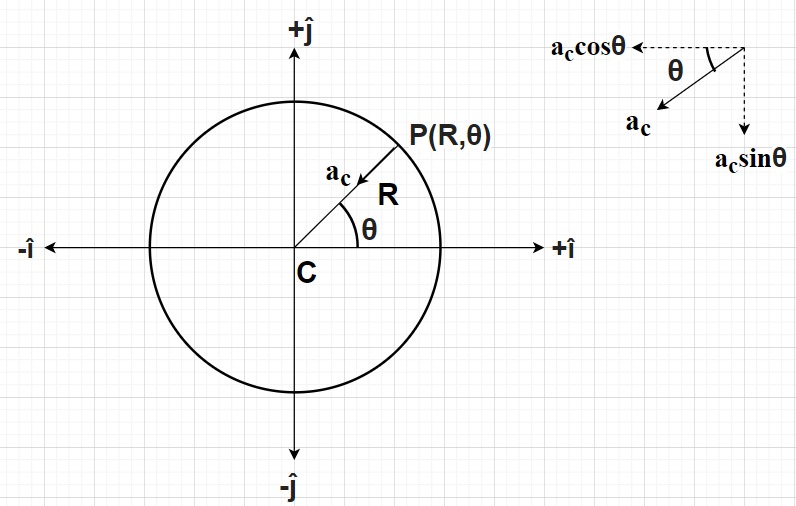
Let us suppose a particle undergoing a uniform circular motion around the circle having radius R as shown in the figure. Let at this particular instant, the particle is at point P(R,$\theta $).
As we know that for any particle to have uniform circular motion, centripetal acceleration towards the centre of the circle should be acting on the particle.
Also, centripetal acceleration experienced by any particle having linear velocity v and radius of the circular motion as R is given by
${a_c} = \dfrac{{{{\text{v}}^2}}}{{\text{R}}}$
This centripetal acceleration will be acting towards the centre of the circle as shown in the figure.
Now, let us resolve this centripetal acceleration into its components acting towards the negative x-axis and negative y-axis as shown in the other figure.
Since, the alternative angles are always equal in measure
The component of the centripetal acceleration acting towards the negative x-axis is equal to \[ - \left( {{a_c}\cos \theta } \right)\widehat i\]
 Similarly, the component of the centripetal acceleration acting towards the negative y-axis is equal to \[ - \left( {{a_c}\sin \theta } \right)\widehat j\]
The total acceleration acting on the particle (in vector form) can be obtained by summing the components of the centripetal acceleration acting on the particle
Acceleration at the point P(R,$\theta $), $
  \overrightarrow a = - \left( {{a_c}\cos \theta } \right)\widehat i + \left[ { - \left( {{a_c}\sin \theta } \right)\widehat j} \right] \\
   \Rightarrow \overrightarrow a = - \left( {{a_c}\cos \theta } \right)\widehat i - \left( {{a_c}\sin \theta } \right)\widehat j \\
 $
By substituting ${a_c} = \dfrac{{{{\text{v}}^2}}}{{\text{R}}}$ in the above equation, we get
$ \Rightarrow \overrightarrow a = - \left( {\dfrac{{{{\text{v}}^2}}}{{\text{R}}}\cos \theta } \right)\widehat i - \left( {\dfrac{{{{\text{v}}^2}}}{{\text{R}}}\sin \theta } \right)\widehat j$
Therefore, option C is correct.

Note- Uniform circular motion at a constant velocity can be defined as the motion of an object in a circle. As an object moves around in a circle, its direction is constantly changing. The object is moving tangent to the circle at all instances. Since the direction of the velocity vector is identical to that of the motion of the object, the velocity vector is also directed tangent to the circle.