Question

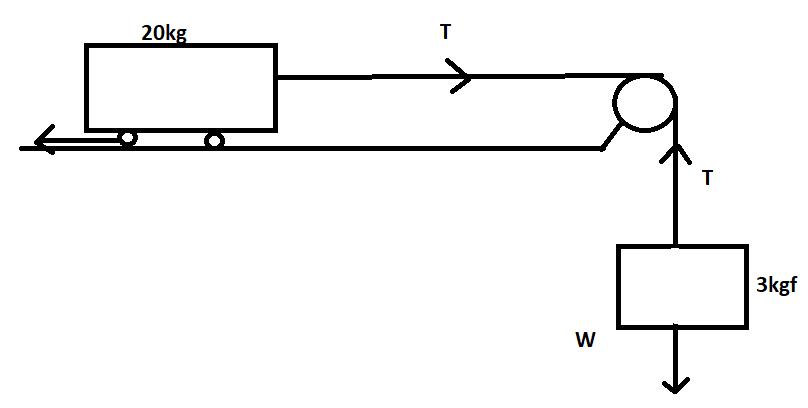
What is the acceleration of the block and trolley system shown in fig. if the coefficient of kinetic friction between the trolley and the surface is \[0.04\]? What is the tension in the string? (take \[g=10\dfrac{m}{{{s}^{2}}}\]). Neglect the mass of the string.

Answer 1

Hint: To solve the given question we will use the formula of force of kinetic friction and also the relationship between the tension of the sting, mass and acceleration so that we can find the acceleration of the block and trolley system and also the tension present in the string.

Complete step-by-step solution:
In the given question we have to find the acceleration of the block and trolley system if the coefficient of kinetic friction between the trolley and the surface is\[0.04\]. Also, we have to find the tension in the string. If we neglect the mass of the string.
Let us first discuss what kinetic friction is?
Kinetic friction can be defined as the force that is acting between the moving surfaces. A body that is moving on the surface experiences a force in the opposite direction of its current movement. The magnitude of the kinetic force will depend on the coefficient of kinetic friction between the two materials.
The formula of force of kinetic friction is coefficient of kinetic friction multiplied by normal force that is as follows:
\[{{F}_{k}}={{\mu }_{k}}\eta \]
Where, \[{{F}_{k}}\]is the force of kinetic friction \[{{\mu }_{k}}\]is the coefficient of kinetic friction and \[\eta \]is the normal force.
Now, let us solve the given question:
Kinetic coefficient of friction is given by the symbol \[{{\mu }_{k}}\]here kinetic coefficient of friction is equal to \[0.04\]
According to the equation for the block
\[30-T={{m}_{1}}a\]
Where \[T\]is tension in the string also \[{{m}_{1}}\]is the mass of the block and \[a\] is the acceleration.
\[30-T=3\times a.....(i)\]
Equation for the trolley,
\[30-{{F}_{k}}={{m}_{2}}a.....(ii)\]
Where \[{{m}_{2}}\]the mass of the trolley, \[a\]is the acceleration and \[{{F}_{k}}\]is the force of kinetic friction.
But we know that \[{{F}_{k}}={{\mu }_{k}}\eta \]
\[{{F}_{k}}=0.04\times 20\times 10\]
\[\begin{align}
  & \eta ={{m}_{2}}g \\
 & =20\times 10 \\
\end{align}\]
\[{{F}_{k}}=8N\]
\[T-8=20\times a.....equation(iii)\]
On adding equation (i) and (ii)
\[\begin{align}
  & 30-8=23\times a \\
 & a=\dfrac{22}{23} \\
\end{align}\]
\[a=0.956\dfrac{m}{{{s}^{2}}}\]
So, we can say that acceleration of the block and trolley system is \[0.956\dfrac{m}{{{s}^{2}}}\]
Now to find the tension in the string,
\[\begin{align}
  & T=20\times a+8 \\
 & T=27.1N \\
\end{align}\]
So, the tension in the string is \[27.1N\]

Note:There are some major applications of kinetic friction like kinetic friction is majorly responsible for the wear and tear of machine parts, that’s why it is very essential to lubricate the machine parts with oil. Also when two objects rub against each other, the frictional force is produced which is converted into thermal energy, and sometimes gives rise to fire.