Question

What is acceleration of centre of mass of system at the instant of maximum elongation of spring:
\[\begin{align}
  & A.0 \\
 & B.\dfrac{F({{m}_{1}}+{{m}_{2}})}{{{m}_{1}}{{m}_{2}}} \\
 & C.\dfrac{F}{{{m}_{1}}} \\
 & D.\dfrac{F}{({{m}_{1}}+{{m}_{2}})} \\
\end{align}\]

Answer 1

Hint: We know that the spring constant is the minimum force which must be applied on the spring to disturb the equilibrium of the spring. This force then displaces the spring from its equilibrium position. Hooke's law gives the relationship between the displacements of the spring the external force applied.

Formula used: $F=-kx$

Complete step by step answer:
We know that when an external force $F$ is applied to a spring it produces a harmonic oscillation. The force applied on a spring produces a displacement $x$.
We also know from Hooke’s law that the magnitude of the force is directly proportional to the displacement of the spring. It is mathematically given as $F=-kx$, $k$ is the spring constant. It is also the force applied on the spring to produce unit displacement. The negative sign indicates that the spring resists the applied force.
Let us assume that the spring acts like a thread, and there are two blocks attached by the spring with mass $m_{1}$ and $m_{2}$ respectively as shown below.

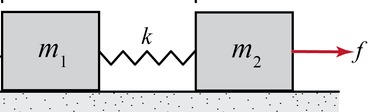
Then the total force acting on the body when acceleration $a$ is applied on the system is given as $F=m_{1}a+m_{2}a$
$\implies a=\dfrac{F}{m_{1}+m_{2}}$

So, the correct answer is “Option D”.

Additional Information: We know that there are two types of forces, namely the normal force plays an important role in the friction it is used to define the Coefficient of static friction. Also, Coefficient of static friction is a dimensionless quantity, $\mu_{s}$ is the maximum resistive force applied on any given body such that there is no change in state of the motion. It is given as $\mu_{s}=\dfrac{F_{s}}{F_{n}}$, where $F_{s}$ is the applied force and $F_{n}$ is the normal force acting on the given body.

Note: The force on the spring is either due to the compression or due to the extension of the spring. We can say that $k$ is a restoring force which tries to restore the spring to its equilibrium position. The spring constant is expressed in terms of $N/m$.