Question

What is the acceleration of a particle moving with velocity 5m/s towards the East and in 10 seconds changing to 5m/s towards North?
A. $ \sqrt 2 {\text{ m/}}{{\text{s}}^{\text{2}}} $ N-W
B. $ \dfrac{1}{{\sqrt 2 }}{\text{ m/}}{{\text{s}}^{\text{2}}} $ N-W
C. $ \dfrac{1}{{\sqrt 2 }}{\text{ m/}}{{\text{s}}^{\text{2}}} $ N-E
D. $ \sqrt 2 {\text{ m/}}{{\text{s}}^{\text{2}}} $ N-E

Answer 1

Hint
To find the acceleration when velocity changes direction, the concept of vector addition is used. The direction of the resultant vector is the direction of the acceleration.
$\Rightarrow a = \dfrac{V}{t} $ where $ a $ is the acceleration, $ V $ is the velocity and $ t $ is the time.

Complete step by step answer
Velocity is a vector which implies that it has a direction along with a magnitude. When a body changes the direction of velocity, the resultant direction is not the same as the current velocity direction and the magnitude of average velocity also changes. Vector addition is used to find the magnitude and direction of the resultant in such a case.
In this question, we are provided with the following data:
Initial velocity $ {V_1} = 10m/s $ in the East direction
Final velocity $ {V_2} = 10m/s $ in the North direction
Time $ t = 10s $
We know that the magnitude of acceleration is given by:
$\Rightarrow a = \dfrac{V}{t} $
To find the average velocity $ V $ , we use the rules of vector addition to find the resultant as:
$\Rightarrow {V_R} = \sqrt {V_1^2 + V_2^2} $
Where $ {V_R} $ is the resultant for two velocities: $ {V_1} $ and $ {V_2} $ .
Now, putting the values as specified in the question, we get:
$\Rightarrow {V_R} = \sqrt {{5^2} + {5^2}} $
$\Rightarrow {V_R} = \sqrt {{5^2}(1 + 1)} $
Taking the square out of the root gives us:
$\Rightarrow {V_R} = 5\sqrt 2 m/s $
To find the acceleration, we put divide this value by time:
$\Rightarrow a = \dfrac{{5\sqrt 2 }}{{10}} $
$\Rightarrow a = \dfrac{{\sqrt 2 }}{2}$
Splitting the denominator further into square roots, we get:
$\Rightarrow a = \dfrac{{\sqrt 2 }}{{\sqrt 2 \times \sqrt 2 }} $
$\Rightarrow a = \dfrac{1}{{\sqrt 2 }}m/{s^2} $
This gives us the magnitude of the acceleration. For the direction, refer to the diagram given below:

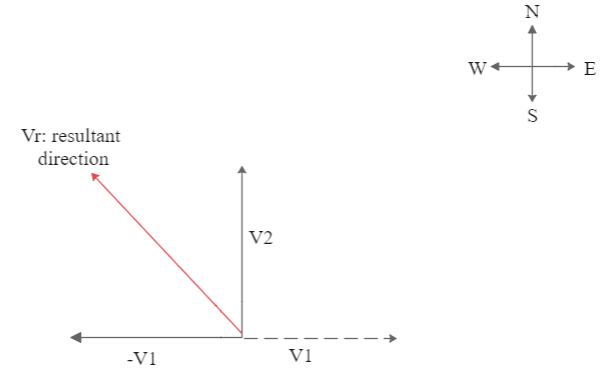
We know that difference of final velocity and initial velocity gives us the change in velocity for an object. As the direction for $ {V_1} $ is East, the direction for $ - {V_1} $ will be West. This gives us the resultant velocity, and simultaneously the acceleration, direction as North-West.
$ \therefore $ The answer is option (B): $ \dfrac{{\text{1}}}{{\sqrt {\text{2}} }}{\text{ m/}}{{\text{s}}^{\text{2}}} $ N-W.

Note
An important concept to remember in these types of questions is that velocities do not add linearly when they are not in the same direction. Also, the direction of the three vectors should be aligned in the correct end to end manner to get the right direction.