Question

∆ABC~∆PQR. If A(∆ABC)=25 , A(∆PQR)=16, find AB:PQ?
A. 25:16
B. 4:5
C. 16:25
D. 5:4

Answer 1

Hint: We are given with two similar triangles and their areas we have to find the ratio of their respective sides. We need to understand when two triangles are similar, when their corresponding angles are equal and their corresponding sides are proportional. We have certain criteria for similarity such as AAA(i.e corresponding angles are equal), SSS( i.e corresponding sides are proportional) etc.

Complete step by step solution:
We have been given that
∆ABC~∆PQR and
ar(∆ABC)=25 and ar(∆PQR)

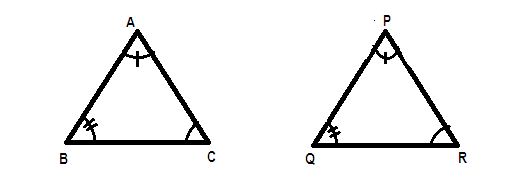
Now we have already seen that in two similar triangles, the ratio of their corresponding sides is the same. We must also know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides from a theorem of similarity in triangles. Therefore if (∆ABC) is similar to (∆PQR) then
$
\Rightarrow \dfrac{{AB}}{{PQ}} = \dfrac{{AC}}{{PR}} = \dfrac{{BC}}{{QR}} \\
  \because \dfrac{{ar(\Delta ABC)}}{{ar(\Delta PQR)}} = \dfrac{{A{B^2}}}{{P{Q^2}}} = \dfrac{{A{C^2}}}{{P{R^2}}} = \dfrac{{B{C^2}}}{{Q{R^2}}} \\
$
Since we just have to find the ratio of side AB to side PQ therefore it can be calculated as,
$\Rightarrow \dfrac{{ar(\Delta ABC)}}{{ar(\Delta PQR)}} = \dfrac{{A{B^2}}}{{P{Q^2}}}$
Substituting the values from the question of the area of the respective similar triangles,
 $
\Rightarrow \dfrac{{25}}{{16}} = \dfrac{{A{B^2}}}{{P{Q^2}}} \\
\Rightarrow \dfrac{{25}}{{16}} = {\left( {\dfrac{{AB}}{{PQ}}} \right)^2} \\
\Rightarrow \sqrt {\dfrac{{25}}{{16}}} = \left( {\dfrac{{AB}}{{PQ}}} \right) \\
\Rightarrow \sqrt {\dfrac{{{5^2}}}{{{4^2}}}} = \left( {\dfrac{{AB}}{{PQ}}} \right) \\
\Rightarrow \left( {\dfrac{{AB}}{{PQ}}} \right) = \dfrac{5}{4} \\
$
(Square rooting both the sides the square from the ratio of sides get cancelled to root)
Therefore we get the ratio of both the sides from their corresponding similar triangles for $AB:PQ = 5:4.$

Note: AA similarity is a corollary to the AAA similarity, it is stated as’ if two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar. The above stated theorem has triangles similar under this criterion. Although having two angles equal leads to the third equal angle as well.