Question

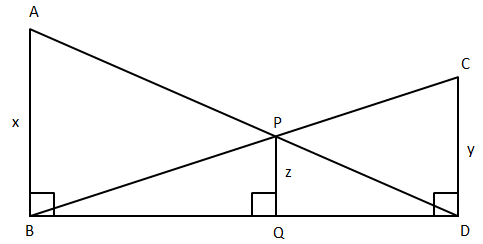
$AB,CD,PQ$ are perpendicular to $BD$. If $AB = x$, $CD = y$ and $PQ = z$
Prove that $\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{z}$

Answer 1

Hint:
Here, we will first prove that the triangles are similar. We will then find the proportion of their corresponding sides. Equating the set of ratios of two corresponding similar sides, we will be able to form a linear equation. We will solve the equation further to prove the required relation.

Complete step by step solution:
Given: $AB,CD,PQ$ are perpendicular to $BD$
Also, $AB = x$, $CD = y$ and $PQ = z$
To prove: $\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{z}$
Proof:
In $\vartriangle ABD$ and $\vartriangle PQD$,
$\angle ADB = \angle PDQ$ (Common angle)
$\angle BAD = \angle QPD$ (Corresponding angles)
Therefore, by Angle-angle or AA Similarity,
$\vartriangle ABD \sim \vartriangle PQD$
Now, when two triangles are similar then their corresponding sides are proportional.
Therefore,
$\dfrac{{AB}}{{PQ}} = \dfrac{{BD}}{{QD}}$
Substituting $AB = x$, $PQ = z$ and $BD = BQ + QD$ in the above equation, we get
Hence, this ratio can be written as:
$ \Rightarrow \dfrac{x}{z} = \dfrac{{BQ + QD}}{{QD}}$
Splitting the denominator in the RHS, we get,
$ \Rightarrow \dfrac{x}{z} = \dfrac{{BQ}}{{QD}} + \dfrac{{QD}}{{QD}}$
$ \Rightarrow \dfrac{x}{z} = \dfrac{{BQ}}{{QD}} + 1$
Subtracting 1 from both the sides, we get
$ \Rightarrow \dfrac{x}{z} - 1 = \dfrac{{BQ}}{{QD}}$
Taking LCM on the LHS, we get
$ \Rightarrow \dfrac{{x - z}}{z} = \dfrac{{BQ}}{{QD}}$…………………………………..$\left( 1 \right)$
Similarly,
In $\vartriangle CBD$ and $\vartriangle PBQ$,
$\angle CBD = \angle PBQ$ (Common angle)
$\angle BCD = \angle BPQ$ (Corresponding angles)
Therefore, by Angle-angle or AA Similarity,
$\vartriangle CBD \sim \vartriangle PBQ$
Now, when two triangles are similar then their corresponding sides are proportional.
Therefore,
$\dfrac{{CD}}{{PQ}} = \dfrac{{BD}}{{BQ}}$
Substituting $CD = y$, $PQ = z$ and $BD = BQ + QD$ in the above equation, we get
Hence, this ratio can be written as:
$ \Rightarrow \dfrac{y}{z} = \dfrac{{BQ + QD}}{{BQ}}$
Splitting the denominator in the RHS, we get,
$ \Rightarrow \dfrac{y}{z} = \dfrac{{BQ}}{{BQ}} + \dfrac{{QD}}{{BQ}}$
$ \Rightarrow \dfrac{y}{z} = 1 + \dfrac{{QD}}{{BQ}}$
Subtracting 1 from both the sides, we get
$ \Rightarrow \dfrac{y}{z} - 1 = \dfrac{{QD}}{{BQ}}$
Taking LCM on the LHS, we get
$ \Rightarrow \dfrac{{y - z}}{z} = \dfrac{{QD}}{{BQ}}$
Taking the reciprocal, we get
$ \Rightarrow \dfrac{z}{{y - z}} = \dfrac{{BQ}}{{QD}}$…………………………………..$\left( 2 \right)$
Now, equating the values of $\dfrac{{BQ}}{{QD}}$ from $\left( 1 \right)$ and $\left( 2 \right)$, we get,
$\dfrac{{x - z}}{z} = \dfrac{z}{{y - z}}$
Cross multiplying, we get
$ \Rightarrow \left( {x - z} \right)\left( {y - z} \right) = {z^2}$
Opening the brackets by multiplying each term of the first bracket by each term of the second bracket, we get,
$ \Rightarrow xy - xz - yz + {z^2} = {z^2}$
Cancelling out the same terms and taking the term which are subtracting to the RHS, we get,
$ \Rightarrow xy = xz + yz$
Dividing both sides by $xyz$, we get
$ \Rightarrow \dfrac{{xy}}{{xyz}} = \dfrac{{xz}}{{xyz}} + \dfrac{{yz}}{{xyz}}$
$ \Rightarrow \dfrac{1}{z} = \dfrac{1}{y} + \dfrac{1}{x}$

Therefore, $\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{z}$
Hence, proved

Note:
In this question, we are given some lines which are perpendicular to a particular line. Now, when two distinct lines intersect each other at $90^\circ $ or form a right angle with each other, they are known as perpendicular. Parallel lines are those lines which are in the same plane and are at the equal distance from each other but they can never meet. Perpendicular lines can’t be parallel and parallel lines can’t be perpendicular to each other.