Question

ABCD is a wire frame of identical wires in which point D is given a velocity v as shown in the figure. Choose the correct statement(s)

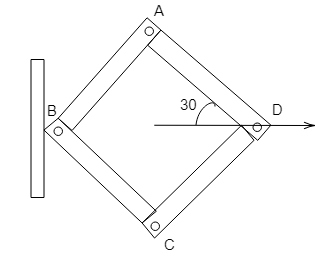
(A) Velocity of point $A$ along the x-axis will be $\dfrac{v}{2}$
(B) Speed of point $A$ will be $v$
(C) Speed of point $A$ along the y-axis will be $\dfrac{v}{2}$
(D) velocity of point $A$ will be equal to velocity of the point $C$

Answer 1

Hint: We know that the angle made at the point $D$ is ${30^o}$, so the angle made at the point $A$ will also be ${30^o}$ due to the property of alternate interior angles. Now, we will resolve the velocity at the point $A$ into the x-component and the y-component and hence get the answer.

Complete step by step solution:

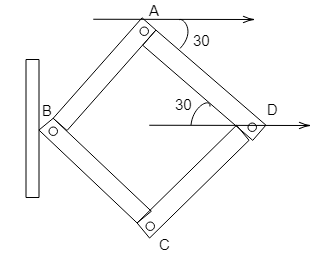
As we can clearly see in the diagram the velocity $v$ of the point $D$ will get transferred to the frame of the wire at the point $A$.
Now, the speed of the point $A = v.......(1)$
The x-component of the velocity at the point $A$ is,
${v_x} = v\cos {30^ \circ }$
On putting the value of \[\cos {30^ \circ }\], we get,
${v_x} = \dfrac{{\sqrt 3 v}}{2}$
The y-component of the velocity at the point $A$ is,
${v_y} = v\sin {30^ \circ }$
On putting the value of $\sin {30^ \circ }$, we get, ${v_y} = \dfrac{v}{2}......(2)$
From equation (1) and (2), we can say that the speed of point $A$ will be $v$ and the speed of point $A$ along the y-axis will be $\dfrac{v}{2}$.
Thus, option (B) and option (C) is the correct answer.

Note:
When an object moves in a projectile motion, then it has two components of velocity vector. The horizontal velocity component ${v_x}$ acts in a way such that it displaces the projectile horizontally. On the other hand, the vertical velocity component ${v_y}$ acts in a way such that it displaces the projectile vertically.