Question

ABCDEFGH is a regular octagon. M is the midpoint of BF. How do you prove that triangles AMG and BDF are similar?

Answer 1

Hint: In this question, we are asked to prove that the two triangles in the octagon are similar, in solving these type of questions we should know the properties of regular octagon i.e., eight congruent exterior angles must be equal to ${45^\circ}$, and eight congruent sides are also equal, and midpoint in the octagon has its eight vertices at the midpoints of the sides of the reference octagon.

Complete step-by-step solution:
 A polygon is a closed shape that is plane and described by joining the finite number line segments to form a closed figure.
An Octagon is a polygon which has eight sides and eight angles.
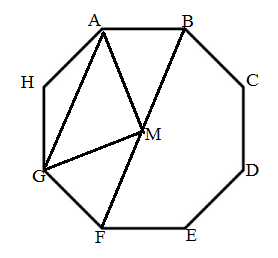
Given that ABCDEFGH is a regular octagon. M is midpoint of BF

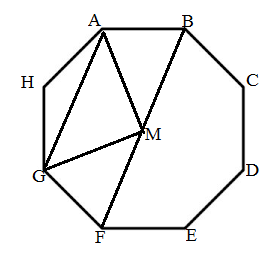
From the diagram it is clear that M is the centre of the regular octagon, and from properties of octagon eight congruent exterior angles are equal to ${45^\circ}$ and eight congruent sides are equal so, from the figure,
$\angle AMB = \angle BMC = \angle GMH = \angle HMA = {45^\circ}$,

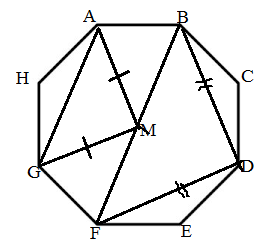
So from the above we can say that $\angle AMG = 2 \times {45^\circ} = {90^\circ}$, and as AM=GM are equal, we can say that $\Delta AMG$ is an isosceles right triangle,
So similarly from the above we can say that $\angle BMD = 2 \times {45^\circ} = {90^\circ}$, and as BM=DM are equal, we can say that $\Delta BMD$ is an isosceles right triangle, and
So similarly from the above we can say that $\angle FMD = 2 \times {45^\circ} = {90^\circ}$, and as FM=DM are equal, we can say that $\Delta FMD$ is also an isosceles right triangle,

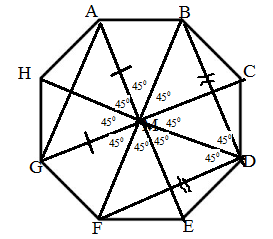
Now from the figure, it is clear that,
$ \Rightarrow \angle MDB = \angle MDF = {45^\circ}$,
From the above, we get,
$ \Rightarrow \angle BDF = \angle MDB + \angle MDF = {45^\circ} + {45^\circ} = {90^\circ}$,
Now from the above it is clear that, BD=FD and $\angle BDF = {90^\circ}$, so $\Delta BDF$ is an isosceles triangle.
Hence from the above, we can state that $\Delta BDF$ and $\Delta AMG$ are similar triangles.
Hence proved.

Note: An octagon is a polygon with eight sides’ .Regular octagons do not have parallel sides. To be a regular octagon the octagon must have some properties and they are:
Eight congruent sides are equal.
Eight congruent interior angles must be equal to ${135^\circ}$.
Eight congruent exterior angles must be equal to ${45^\circ}$.
It has 20 diagonals.