Question

ABCDEFG is a regular heptagon. Then, which of the following is/are true?
$\left( a \right)\dfrac{1}{{{\text{AB}}}} = \dfrac{1}{{{\text{AC}}}} - \dfrac{1}{{{\text{AD}}}}$
$\left( b \right)\dfrac{1}{{{\text{AB}}}} = \dfrac{1}{{{\text{AC}}}} + \dfrac{1}{{{\text{AD}}}}$
$\left( c \right)\dfrac{1}{{{\text{2AB}}}} = \dfrac{1}{{{\text{AC}}}} + \dfrac{1}{{{\text{AE}}}}$
$\left( d \right)\dfrac{1}{{{\text{AB}}}} = \dfrac{1}{{{\text{AC}}}} - \dfrac{1}{{{\text{AE}}}}$

Answer 1

Hint: In this particular question use the concept that in a regular polygon all sides are equal to each other, a line joining first and third vertices are taken in order are always equal and the line joining first and fourth vertices taken in order are always equal and so on in a regular polygon, and use the property of cyclic quadrilateral Ptolemy’s theorem so use these concepts to reach the solution of the question.

Complete step-by-step solution:
The regular ABCDEFG is shown below in the diagram.

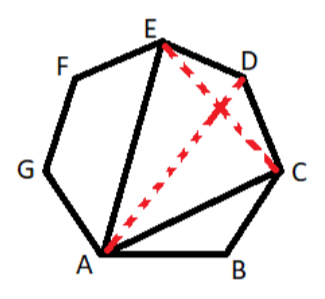
Now as we know in a regular polygon all sides are equal to each other, the line joining first and third vertices taken in order are always equal and the line joining first and fourth vertices taken in order are always equal, and so on.
Therefore, $AB = BC = CD = DE = EF = GA, AC = CE = EG = ....., AE = AD = BE = BF = ....$.
Let, $AB = BC = CD = DE = EF = GA = a$.................. (1)
$AC = CE = EG =..... = b$................ (2)
$AE = AD = BE = BF = ...... = c$ ................. (3)
Now consider a cyclic quadrilateral ACDE as shown in the above figure.
Where AD and CE are the diagonals of the cyclic quadrilateral.
Now let us assume a circle circumscribing the quadrilateral ACDE whose vertices lie on the circle.
So according to Ptolemy’s theorem, the product of the diagonals of the cyclic quadrilateral is equal to the sum of the product of opposite sides of the cyclic quadrilateral.
So apply this theorem in ACDE cyclic quadrilateral we have,
$ \Rightarrow \left( {{\text{AD}}} \right)\left( {{\text{CE}}} \right) = \left( {{\text{AE}}} \right)\left( {{\text{CD}}} \right) + \left( {{\text{AC}}} \right)\left( {{\text{DE}}} \right)$
Now substitute the values we have,
$ \Rightarrow cb = ca + ba$
Now divide by $abc$ throughout we have,
$ \Rightarrow \dfrac{{cb}}{{abc}} = \dfrac{{ca}}{{abc}} + \dfrac{{ba}}{{abc}}$
$ \Rightarrow \dfrac{1}{a} = \dfrac{1}{b} + \dfrac{1}{c}$
Now from equations (1), (2), and (3), we have,
$ \Rightarrow \dfrac{1}{{{\text{AB}}}} = \dfrac{1}{{{\text{AC}}}} + \dfrac{1}{{{\text{AD}}}}$
So this is the required answer.
Hence option (b) is the correct answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall that according to Ptolemy’s theorem the product of the diagonals of the cyclic quadrilateral is equal to the sum of the product of opposite sides of the cyclic quadrilateral, so use this property as above in any cyclic quadrilateral we will get the required answer.