Question

ABCDEF is a regular hexagon. The centre of hexagon is at point O. Then the value of $\vec{AB}+\vec{AC}+\vec{AD}+\vec{AE}+\vec{AF}$ is
A. $2\vec{AO}$
B. $4\vec{AO}$
C. $6\vec{AO}$
D. Zero

Answer 1

Hint: Draw a regular hexagon and locate the vectors given. Then apply the parallelogram law of vector addition to change the given vectors in terms of the vector given in options. Then after changing them, add them all to get the final solution.

Complete step by step solution:
We have been given a regular hexagon ABCDEF with O at its center. And we have to find the value of $\vec{AB}+\vec{AC}+\vec{AD}+\vec{AE}+\vec{AF}$.
Let us draw the hexagon and indicate the given vector,

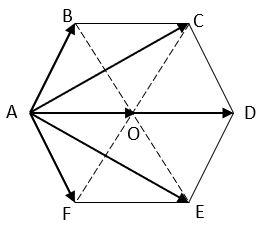
Now, using parallelogram law of vector addition we can write $\vec{AC}=\vec{AB}+\vec{AO}$ ………. (i)
Similarly, $\vec{AE}=\vec{AF}+\vec{AO}$ ………. (ii)
Also, we can notice from the diagram that $\vec{AD}=2\vec{AO}$ ………. (iii)
Using equations (i), (ii) and (iii) in the given problem, we can write
$\vec{AB}+\vec{AC}+\vec{AD}+\vec{AE}+\vec{AF}=\vec{AB}+\vec{AB}+\vec{AO}+2\vec{AO}+\vec{AF}+\vec{AO}+\vec{AF}$
$=2(\vec{AB}+\vec{AF})+4\vec{AO}$
Using parallelogram law of addition, we have $\vec{AB}+\vec{AF}=\vec{AO}$
Therefore, $2(\vec{AB}+\vec{AF})+4\vec{AO}=6\vec{AO}$
Hence, option c is the correct answer.

Additional information:
We generally use two types of vector addition techniques; one is the triangle law and other one is parallelogram law of vector addition.
Triangle law of vector addition states that when we represent two sides of a triangle as two vectors, then the third side will represent the resultant vector of other two vectors. here, the sides represent the direction, order and magnitude.
Parallelogram law of vector addition states that if two vectors are represented by two sides of a parallelogram, then their sum will represent the diagonal vector through their common point.

Note: Both the laws of vector addition should be conceptually clear and once should know when to use what law or else it may lead to confusion. And while applying the laws of vector addition, one should be extra careful in determining which diagonal is formed by adding up which sides.