Question

ABCD is rectangle and P,Q, R and S are midpoint of the sides AB, BC, CD and DA respectively, then the quadrilateral PQRS is rhombus.
a. True
b. False

Answer 1

Hint: We will prove PQRS is a rhombus and choose the true or false accordingly. We will use the midpoint theorem to prove that PQRS is a rhombus and using this we will first prove that PQRS is a parallelogram. In the second step, we will show that the sides PS is equal to side PQ by showing that triangle ASP is similar to triangle BQP. From that we will conclude that PQRS is a rhombus because a parallelogram having all sides as equal is a rhombus.

Complete step-by-step answer:
It is given in the question that ABCD is a rectangle and P, Q, R, S are the midpoints of the sides AB, BC, CD and DA respectively. We have to find whether PQRS is a rhombus or not. We will first draw the rectangle ACBD and plot P, Q, R, S as the midpoints of sides AB, BC, CD and DE respectively. So, we get the figure as below.

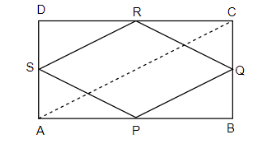
We know that the diagonals of the rectangle are of equal length. And according to the midpoint theorem in triangle, if two sides of a triangle are bisected by a line and it is parallel to the third side of the triangle, then the line is half of the third side. In $ \Delta ACD $ , we have SR as the line that is parallel to side AC. And S is the midpoint of AD and R is the midpoint of DC. So, we get,
 $ SR=\dfrac{1}{2}AC\ldots \ldots \ldots \left( i \right) $
Similarly, in $ \Delta ACB $ , we have PQ parallel to AC and P and Q are the midpoints of sides AB and BC. So, we get,
 $ PQ=\dfrac{1}{2}AC\ldots \ldots \ldots \left( ii \right) $
So, we can say from equations (i) and (ii), we get,
 $ \begin{align}
  & PQ=SR \\
 & \Rightarrow PQ\parallel SR \\
\end{align} $
Similarly, we will get $ RQ=SP\Rightarrow RQ\parallel SP $ . So, we can say that PQRS is a quadrilateral. Now, we know that a quadrilateral having opposite sides as parallel and equal are called parallelograms. Now, we can see that in the quadrilateral PQRS, we have, $ PQ\parallel RS,PS\parallel QR $ and $ PQ=RS,PS=QR $ . Therefore, we can conclude that PQRS is a parallelogram.
Now, in $ \Delta ASP $ and $ \Delta BQP $ , we have,
 $ AS=BQ\ldots \ldots \ldots \left( iii \right) $
We get this as we know that the opposite sides of a rectangle are equal and S and Q are the midpoints of the sides AD and BC. And so we get,
 $ \begin{align}
  & AD=BC \\
 & \Rightarrow \dfrac{1}{2}AD=\dfrac{1}{2}BC \\
 & \Rightarrow AS=BQ \\
\end{align} $
We also know the following,
 $ \angle SAP=\angle QBP=90{}^\circ \ldots \ldots \ldots \left( iv \right) $
And we know that P is the midpoint of side AB, so,
 $ AP=BP\ldots \ldots \ldots \left( v \right) $
So, form equations (iii), (iv) and (v), we get that $ \Delta ASP $ and $ \Delta BQP $ are similar, that is,
 $ \Delta ASP\cong \Delta BQP $
Thus, we get that side $ PS=PQ $ by the CPCT property, where CPCT means corresponding part of the congruent triangle. Now, we know that, $ PS=QR $ and $ PQ=RS $ as PQRS is a parallelogram. So, we now have that,
 $ PS=QR=PQ=RS $
So, we get that all the four sides of the parallelogram PQRS are equal. And we know that a parallelogram having all four sides equal is called a rhombus.
Therefore, the given statement is true.
So, the correct answer is “Option A”.

Note: Many students get confused in the last step after they prove that all the four sides of the parallelogram are equal. They think that a parallelogram with all four sides as equal is called a square, but that is not true as we have to justify that all angles of a square are equal to $ 90{}^\circ $ . That is not required for a rhombus and we cannot label it as a square without justifying that all the angles of the parallelogram are equal to $ 90{}^\circ $ .