Question

ABCD is acyclic quadrilateral whose diagonals intersect at a point E. If $\angle DBC={{70}^{\circ }},\angle BAC={{30}^{\circ }}$, find $\angle BCD$. Further if $AB=BC$, find $\angle ECD$.

Answer 1

Hint:Here, first we have to draw the figure. Then apply the theorem, angles in the same segment are equal, we will get, $\angle DBC=\angle DAC$. Next, find $\angle BAD$. With the help of the theorem that opposite angles of the cyclic quadrilateral are supplementary, we can find $\angle BCD$. Next, to find $\angle ECD$ consider the triangle $\Delta ABC$, where $AB=BC$. Now, by applying the theorem that angles opposite to equal sides are equal, we can find $\angle BCA$. At last find $\angle ECD$ where $\angle BCD=\angle BCA+\angle ECD$.

Complete step by step answer:
First let us draw the figure with the given data.

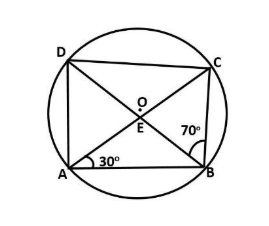
Here, we are given that ABCD is a cyclic quadrilateral whose diagonals intersects at a point E and $\angle DBC={{70}^{\circ }},\angle BAC={{30}^{\circ }}$.
Now, we have to find $\angle BCD$.
We have a theorem that angles in the same segment are equal. So, here consider the chord CD, we have by this theorem:
$\angle DBC=\angle DAC$
We have $\angle DBC={{70}^{\circ }}$, therefore we can say that:
$\angle DAC={{70}^{\circ }}$
Now, let us consider $\angle BAD$, we have:
$\angle BAD=\angle DAC+\angle BAC$
We already have $\angle DAC={{70}^{\circ }}$ and $\angle BAC={{30}^{\circ }}$. Hence, we will get:
$\begin{align}
  & \angle BAD={{70}^{\circ }}+{{30}^{\circ }} \\
 & \angle BAD={{100}^{\circ }} \\
\end{align}$
We know that in a cyclic quadrilateral the opposite angles are supplementary. Since, ABCD is acyclic quadrilateral we have:
$\angle BAD+\angle BCD={{180}^{\circ }}$
We got that $\angle BAD={{100}^{\circ }}$, hence, we will obtain:
${{100}^{\circ }}+\angle BCD={{180}^{\circ }}$
Now, by taking ${{100}^{\circ }}$ to the right side ${{100}^{\circ }}$ becomes ${{100}^{\circ }}$. Therefore, we will get:
$\begin{align}
  & \angle BCD={{180}^{\circ }}-{{100}^{\circ }} \\
 & \angle BCD={{80}^{\circ }} \\
\end{align}$
Hence, we can say that $\angle BCD={{80}^{\circ }}$.
Next, we have to find $\angle ECD$ given that $AB=BC$.
For that consider the triangle $\Delta ABC$, we have $AB=BC$.
We know that the angles opposite to equal sides are equal. Therefore, we can write:
$\angle BCA=\angle BAC$
Since, $\angle BAC={{30}^{\circ }}$, we can write:
$\angle BCA={{30}^{\circ }}$
Now, consider $\angle BCD$, we can write in the form:
$\angle BCD=\angle BCA+\angle ECD$
We have $\angle BCD={{80}^{\circ }}$ and $\angle BCA={{30}^{\circ }}$. Now, by substituting these values in the above equation we get:
 ${{80}^{\circ }}={{30}^{\circ }}+\angle ECD$
Next, by taking ${{30}^{\circ }}$ to the left side, ${{30}^{\circ }}$ becomes $-{{30}^{\circ }}$. Hence, we obtain:
$\begin{align}
  & {{80}^{\circ }}-{{30}^{\circ }}=\angle ECD \\
 & {{50}^{\circ }}=\angle ECD \\
\end{align}$
Hence, we can say that the value of $\angle ECD={{50}^{\circ }}$

Note:Here, ABCD is a cyclic quadrilateral. A cyclic quadrilateral is a quadrilateral whose all four vertices lie in the circumference of the circle. A circle which contains all the vertices of any polygon is called circumcircle. For a cyclic quadrilateral the sum of all four angles is ${{360}^{\circ }}$ and the sum of the opposite angles is ${{180}^{\circ }}$.