Question

ABCD is a trapezium where AB is parallel to CD, measure of $ \angle \left( A \right) = \angle \left( B \right) = {45^ \circ } $ . Prove that AD=BC.

Answer 1

Hint: Here we will discuss the trapezium that we have to prove is an isosceles trapezium. We will also use the result of congruence of triangles and the concept that the distance between the parallel lines are always equal. For this we will draw perpendiculars DE and CF from CD to AB which are given parallel.

Complete step-by-step answer:
Now we are given ABCD is a trapezium, ABǁCD
Draw perpendicular DE and CF on AB

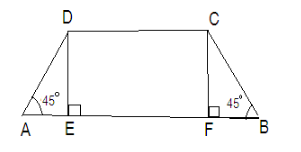
In ∆ADE and ∆BCF
 $ \angle A = \angle B $ (Both are given as $ {45^ \circ } $ )
 $ \angle E = \angle F $ (Both are $ {90^ \circ } $ as they are the base of perpendicular)
DE=CF (As the distance between the parallel lines are always equal)
By AAS congruence rules (that is two angles and one side is equal in both the triangles)
 $
  \Delta ADE \cong \Delta BCF \;
  \therefore AD = BC \;
  $
(As we know that the corresponding parts of congruent triangle are equal)
Hence proved that the above trapezium ABCD is an isosceles triangle.

Additional information: Congruency means that the corresponding angles or sides are equal to each other. Congruence can be of many types in the triangle. When the congruence is due to all the sides being equal, it is SSS congruence. When two sides are equal and one angle is equal then the congruence is of the type SAS. Similarly other congruences can be also thought of.

Note: A trapezium is a type of quadrilateral where one pair of opposite sides are parallel, since this trapezium has its non parallel sides equal i.e. AD=BC as proved above. Such a trapezium is called an isosceles trapezium.