Question

ABCD is a trapezium in which AB $\parallel $ CD; BC and AD are non-parallel sides. It is given that AB = 75cm, BC = 42cm, CD = 30cm and AD = 39cm. Find the area of the trapezium.

Answer 1

Hint: We will use the direct formula to find the area of the trapezium ABCD as $\dfrac{1}{2}\times $ (Sum of parallel sides) $\times $ (Perpendicular distance between them). We will also use Heron’s formula that is$\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$.

Complete step-by-step solution -
It is given in the question that ABCD is a trapezium in which the side AB is parallel to the side CD. Also, side BC and AD are non-parallel sides of the trapezium. It is also given that AB = 75cm, BC = 42cm, CD = 30cm and AD = 39cm. So, we have to find the area of the trapezium ABCD.

From the above figure, we can see that DE is the perpendicular distance between the two parallel sides of the trapezium. Now let us construct a line DF parallel to the side CD, so we will get the figure as shown below,

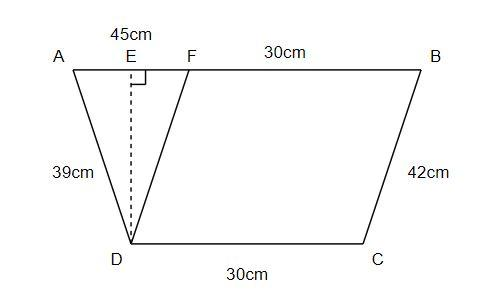
Here, we can see that DCBF is a parallelogram with sides BC = DF = 42cm and BF = CD = 30cm. Also, we know that the side AB is of the length 75cm. So, the length of AF is given by (AB - BF), that is (75 - 30) which is 45cm. Hence, we get the length of AF equal to 45cm. Now, we have a triangle ADF with the sides AD = 39cm, DF = 42cm and AF = 45cm. We know that Heron’s formula is $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$.
Heron’s formula is used to find the area of a triangle when all the sides of the triangle are known. In the formula, s is the semi-perimeter of the triangle which is $\dfrac{a+b+c}{2}$ where, a, b, c are the three sides of the triangle. So we can calculate the area of the triangle ADF using Heron’s formula. Let us take side a (AD) = 39cm, side b (DF) = 42cm and side c (AF) = 45cm. We know that $s=\dfrac{a+b+c}{2}$.
On substituting the values of a, b and c in the formula for s, we get,
$s=\dfrac{39+42+45}{2}$
$s=\dfrac{126}{2}$
$s=63cm$
Now, on substituting the values of s = 63, a = 39, b = 42 and c = 45 in the Heron’s formula, we get,
Area of the triangle (ADF) = $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$
$=\sqrt{63\left( 63-39 \right)\left( 63-42 \right)\left( 63-45 \right)}$
$=\sqrt{63\times 24\times 21\times 18}$
$=\sqrt{571536}$
=$756c{{m}^{2}}$
So, the area of the triangle ADF is $756c{{m}^{2}}$.
Now, we know that the area of the triangle can be calculated as $\dfrac{1}{2}\times base\times height$. We know that the area of triangle ADF is $756c{{m}^{2}}$. So, on equating both the values of area of the triangle, we get,
$\dfrac{1}{2}\times AF\times DE=756\ldots \ldots \ldots (i)$
We know that AF = 45cm, so on substituting the value of AF in equation (i), we get,
$\begin{align}
  & \dfrac{1}{2}\times 45\times DE=756 \\
 & 45DE=756\times 2 \\
 & DE=\dfrac{756\times 2}{45} \\
 & DE=33.6cm \\
\end{align}$
So, the distance between parallel sides of trapezium is 33.6 cm.
We know that, area of the trapezium (ABCD) = $\dfrac{1}{2}\times $ (Sum of parallel sides) $\times $ (Perpendicular distance between them). We have sum of parallel sides as (AD + CD) = (75 + 30) = 105 and the perpendicular distance between the parallel sides as (DE) = 33.6 cm.
So, the area of the trapezium is $\dfrac{1}{2}\times (75+30)\times 33.6c{{m}^{2}}$
$=\dfrac{1}{2}\times 105\times 33.6c{{m}^{2}}$
$=52.5\times 33.6c{{m}^{2}}$
$=1764c{{m}^{2}}$
Therefore, area of the trapezium (ABCD) $=1764c{{m}^{2}}$.

Note: We can also find the area of the trapezium by finding the area of triangle DFA and the area of the parallelogram DCBF and adding them. Area of trapezium (ABCD) = (Area of triangle DFA) + (Area of parallelogram DCBF). We have calculated the area of DFA as $756c{{m}^{2}}$. Area of parallelogram = Base $\times $ Height $=30\times 33.6=1008$. Therefore, the area of the trapezium $=1008+756=1764c{{m}^{2}}$.