Question

ABCD is a trapezium, in which AB is parallel to DC. Diagonal AC and BD intersect each other at O. If $\dfrac{AO}{OC}=\dfrac{BO}{OD}=\dfrac{1}{2}$ and AB = 4cm, find CD.

Answer 1

Hint: In this question, we are given trapezium ABCD and we need to find length CD if $AB\parallel CD$ diagonal AC and BD intersect at O, $\dfrac{AO}{OC}=\dfrac{BO}{OD}=\dfrac{1}{2}$ and AB = 4cm. For this, we will first draw a diagram to understand the question clearly. Then, we will prove similarity of two triangles AOB and COD using AAA similarity condition. We will use properties of lines and angles which are that vertically opposite angles are equal and alternate interior angles are equal. At last, we will use the property of a similar triangle which states that, corresponding sides of similar triangles are proportional to find value of CD.

Complete step-by-step answer:
Let us first draw the diagram to understand the question clearly.

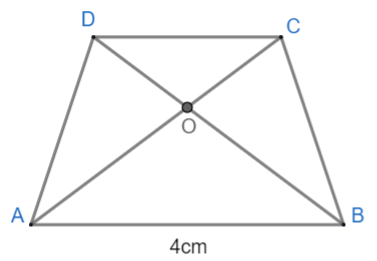
Here we are given trapezium ABCD with $AB\parallel CD$. Diagonal AC and BD intersect each other at O and we need to find the length of CD if AB = 4cm.
As we know that, $AB\parallel CD$ and hence AC acts as a transversal therefore, we get figure of parallel lines with transversal as,

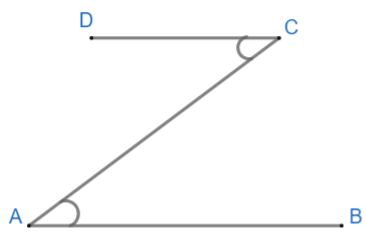
As we can see, $\angle DCA\text{ and }\angle CAB$ form a pair of alternate interior angles. Therefore, they are equal (property of lines and angles states that alternate interior angles are always equal). So,
\[\angle DCA=\angle CAB\ldots \ldots \ldots \left( 1 \right)\]
Now, $AB\parallel CD$ and BD is transversal, so we have:

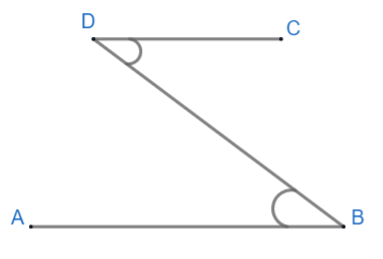
As we can see, $\angle CDB\text{ and }\angle DBA$ are alternate interior angles and hence equal. So,
\[\angle CDB=\angle DBA\ldots \ldots \ldots \left( 2 \right)\]
Also, from the original figure, we can see that AC and BD intersect at O. Therefore, $\angle COD\text{ and }\angle BOA$ forms a pair of vertically opposite angles. As we know, vertically opposite angles are always equal, therefore,
\[\angle COD=\angle BOA\ldots \ldots \ldots \left( 3 \right)\]
Now let us take triangles $\angle AOB\text{ and }\angle COD$. From (1) we can say $\angle DCO=\angle OAB$ and from (2) we can say $\angle CDO=\angle OBA$. Also from (3) $\angle COD=\angle BOA$.
Therefore, all the corresponding angles of the triangle are equal. Hence, by AAA criteria of similarity, $\Delta AOB\text{ and }\Delta COD$ are similar triangles.
Now, we know that, corresponding sides of similar triangle are always proportional, therefore,
$\dfrac{AO}{OC}=\dfrac{BO}{OD}=\dfrac{AB}{CD}$.
As we know, $\dfrac{AO}{OC}=\dfrac{BO}{OD}=\dfrac{1}{2}$ so we get:
$\dfrac{AB}{CD}=\dfrac{1}{2}$.
Also we know that AB = 4cm so we get:
$\dfrac{4}{CD}=\dfrac{1}{2}$.
Cross multiplying we get:
$8=CD$.
Hence CD = 8cm.

Note: Students should keep in mind all the properties of lines and angles, similar triangles to solve this question. While taking transversal, students can get confused between angles, so they should always draw separate diagrams for parallel lines with their transversal. Since AB is given in cm so don't forget to put units for CD as well.