Question

ABCD is a square with side ‘a’. With centres A, B, C and D four circles are drawn such that each circle touches externally two of the remaining three circles and all have the same radius. Find the area of the region in the interior of the square and exterior of the circles:
(A). ${{a}^{2}}\left( 1-\pi \right)$
(B). ${{a}^{2}}\left( \dfrac{4-\pi }{4} \right)$
(C). ${{a}^{2}}\left( \pi -1 \right)$
(D). $\dfrac{\pi {{a}^{2}}}{4}$

Answer 1

Hint: First we will draw the diagram and with that we will find the radius of the circle in terms of ‘a’ and then we will subtract the area of intersection of all four circles with the square and that will be our final answer.

Complete step-by-step solution -
First let’s look at the figure,

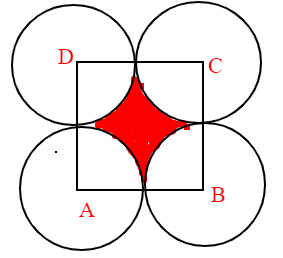
R = radius of circle.
Now as per the question the radius of all four circles are the same and they touch each other so the sum of the radius of two circles must be equal to the side of square ‘a’.
Hence 2R = a
$R=\dfrac{a}{2}$
So, now we have find the radius of circle in terms of ‘a’,
Now the area of intersection between square and circle is:
4 times area of each circle intersected by square.
And the area intersected by square and one circle will be $\dfrac{1}{4}\times $ area of cirle
Area of circle is $\pi {{\left( \dfrac{a}{2} \right)}^{2}}$
$\begin{align}
  & 4\times \dfrac{\pi }{4}{{\left( \dfrac{a}{2} \right)}^{2}} \\
 & =\dfrac{\pi {{a}^{2}}}{4} \\
\end{align}$
Area of square = ${{a}^{2}}$
 Now the area interior of the square and exterior of the circles is:
Area of square – area of circles intersected with square
$\begin{align}
  & ={{a}^{2}}-\dfrac{\pi {{a}^{2}}}{4} \\
 & ={{a}^{2}}\left( \dfrac{4-\pi }{4} \right) \\
\end{align}$
Hence option (b) is correct.

Note: The diagram for this question is very important and with that one can get the clear picture of what is happening in the question and what we have to find. And the formulas should be used carefully while calculating the values.