Question

$ABCD$ is a square with each side 12 cm. $P$ is a point on BC such that area of
$\Delta ABP$: area of trapezium $APCD = 1:5$. Find the length of $CP$.
E. 1
F. 5
G. 8
H. 10

Answer 1

Hint: First we have to find the area of the triangle and the area of the trapezium. Since the ratio
of the area of the triangle to the area of the trapezium is given, we have to substitute the values of
area of the triangle and the trapezium, which will give us an algebraic expression for their ratio.
After that we have to solve the expression for $CP$ which will give us the required length of
$CP$.

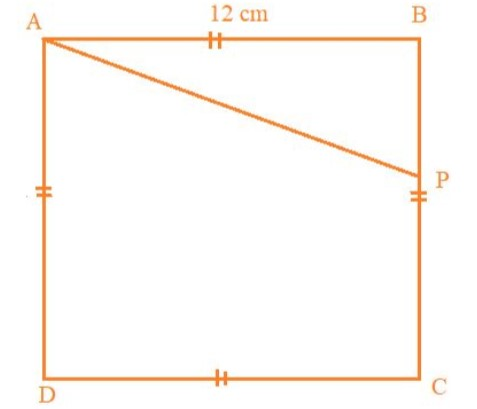
Given that the side of the square $ABCD$ is 12 cm and the point $P$ on the side $BC$.
Find the area of the triangle $\Delta ABP$.
Substituting 12 for AB in the formula of area of the triangle.

$\begin{array}{c}{\rm{Are}}{{\rm{a}}_{\left( {\Delta ABP} \right)}} = \dfrac{1}{2} \times
AB \times BP\\ = \dfrac{1}{2} \times 12 \times BP\\ = 6BP\end{array}$

Find the area of the trapezium $APCD$.
Substituting 12 for AD and 12 for CD in the formula of area of the trapezium.
$\begin{array}{c}{\rm{Are}}{{\rm{a}}_{\left( {APCD} \right)}} = \dfrac{1}{2} \times \left(
{AD + CP} \right) \times CD\\ = \dfrac{1}{2} \times \left( {12 + CP} \right) \times 12\\ = 6
\times \left( {12 + CP} \right)\end{array}$
It is given that the ratio of the area of the triangle to the area of the trapezium$ = \dfrac{1}{5}$
$\begin{array}{c}\therefore \dfrac{{{\rm{Are}}{{\rm{a}}_{\left( {\Delta ABP}
\right)}}}}{{{\rm{Are}}{{\rm{a}}_{\left( {APCD} \right)}}}} = \dfrac{1}{5}\\ \Rightarrow
\dfrac{{6BP}}{{6\left( {12 + CP} \right)}} = \dfrac{1}{5}\\ \Rightarrow \dfrac{{BP}}{{12 +
CP}} = \dfrac{1}{5}\\ \Rightarrow 5BP = 12 + CP\end{array}$ ……
(1)

Since $BC = BP + CP$
$ \Rightarrow BP = BC - CP$

Substituting $BC - CP$ for $BP$ in the equation (1).
$\begin{array}{c}5\left( {BC - CP} \right) = 12 + CP\\5BC - 5CP = 12 + CP\end{array}$

Substitute 12 for BC in the above equation and simplify.
$\begin{array}{c}5 \times 12 - 5CP = 12 + CP\\6CP = 48\\CP = 8\end{array}$

Thus, the required length of $CP$ is 8 cm.
Hence, the correct option is C.

Note: Here we have to determine the length of $CP$ for the given information. From the figure
we can calculate the area of the triangle and the area of the trapezium. Since the ratio of the area
of the triangle to the area of the trapezium is given, we can find the required length of the $CP$
by taking the ratio of their respective areas.