Question

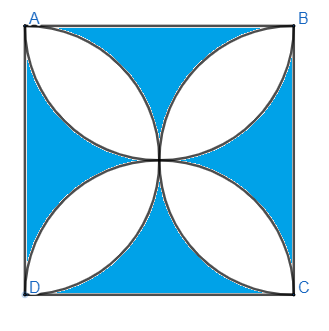
ABCD is a square of side \[14cm\]. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.

Answer 1

Hint: In the given question, we are asked to find the area of the shaded region. We will first find the area of the square ABCD with side \[14cm\]. We will then name the shaded region and find the area of the 4 semi circles that we are given in the question. Then we will subtract the area of the four semicircles with the area of the square. hence, we will have the required area of the shaded region.

Complete step by step solution:
According to the given question, we are given a square ABCD and inside it are four semicircles and we have to find the area of the shaded region.
We will first find the area of the square.
We know that, the formula for area of the square is \[sid{{e}^{2}}\], so we have,
\[\Rightarrow {{14}^{2}}\]
\[\Rightarrow 196c{{m}^{2}}\]
Now, we will mark the region as I, II, III and IV. We will have the figure as follows,

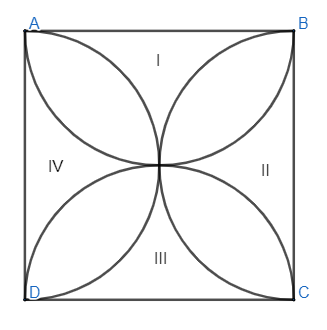
So, as we can see that there four semicircles and we have the diameter of these semicircles as,
\[=14cm\]
So, the radius \[=\dfrac{14}{2}=7cm\]
We will now find the area of the semicircle, which is, \[\dfrac{1}{2}\pi {{r}^{2}}\]
Substituting the value of radius, we get the area as,
\[\Rightarrow \dfrac{1}{2}\left( \dfrac{22}{7} \right){{\left( 7 \right)}^{2}}\]
Cancelling out the common terms, we will get,
\[\Rightarrow 11\times 7=77c{{m}^{2}}\]
Since the square has all equal sides so the diameter of all the four semicircles are the same and so are their radii. Therefore, each semicircle has the area as \[77c{{m}^{2}}\].
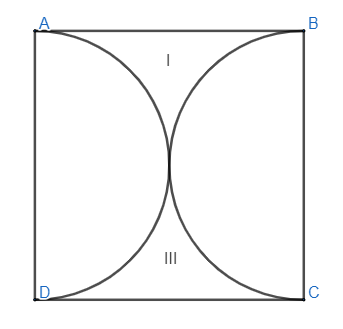
We will first find the area of the region I and III and so it will be equal to,
Area of the square – (Area of the semicircle AD and BC) -----(1)
The figure for the same is as follows.

Similarly, to find the area of the region II and IV, we will write,
Area of the square – (Area of the semicircle AB and DC) -----(2)
Adding up the equation (1) and equation (2), we get,

Area of the regions I, II, III and IV
= 2(Area of the square) – (Area of the semicircle AB, BC, DC and AD)
We will now substitute the values of the known terms and we get,
\[=2(196)-(77+77+77+77)\]
Multiplying the terms and solving it further, we get,
\[=392-(77\times 4)\]
\[=392-308\]
So, we get the value as,
\[=84c{{m}^{2}}\]
Therefore, the area of the shaded region is \[84c{{m}^{2}}\].

Note: In the above solution, we took the regions separately as it will be easier to solve that way. If we were to take all the semicircles together at the very beginning, the entire answer will seem very hard to proceed and also will be difficult to understand. It is advised to always carry out these questions in parts so that it is easier to solve as well as to understand.