Question

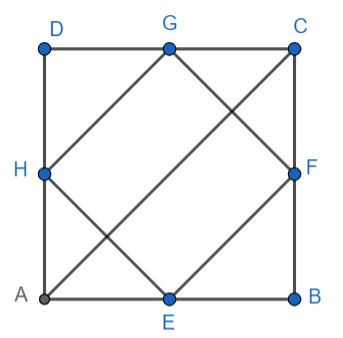
ABCD is a square. E, F, G and H are the midpoints of AB, BC, CD and AD respectively. Prove that EFGH is square.

Answer 1

Hint: Use the converse of the midpoint theorem to prove that EFGH is a rhombus. Then prove one angle of EFGH is right and hence prove that EFGH is square. Think why one angle of rhombus being right means the rhombus is a square.

Complete step-by-step answer:
Before solving the question, we need to understand the definitions of the midpoint theorem and the converse of the midpoint theorem.
Consider the triangle ABC as shown in the diagram below.
Suppose that D is the midpoint of AB.

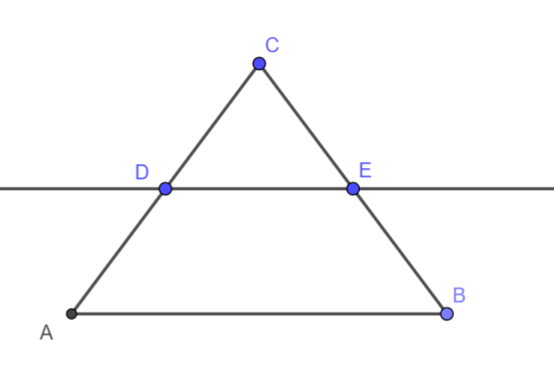
The midpoint theorem says that if DE is parallel to AB then E is the midpoint of BC and $DE=\dfrac{1}{2}AB$. The statement of the theorem is
“ A line from the midpoint of one side of a triagle parallel to another side bisects the third side. The line segment contained inside the triangle is half of the side of the triangle to which it is parallel”
The converse of the midpoint says that if E is the midpoint of BC then DE is parallel to AB and $DE=\dfrac{1}{2}AB$.
The statement of the converse is
“ The line segment joining midpoints of two sides of a triangle is parallel to the third side and is one half of it”
Given: A square ABCD. E, F, G and H are the midpoints of AB, BC, CD and AD respectively.
To prove: EFGH is a square.
Construction: Join AC.
Proof:
In triangle ADC, G is the midpoint of CD and H is the midpoint of AD.
We know that in a triangle the line segment joining midpoints of two sides of a triangle is parallel to the third side and one half of it.
Hence by the converse of midpoint theorem, GH||AC and $\text{GH=}\dfrac{1}{2}\text{AC}$.
Similarly FE||AC and $\text{FE=}\dfrac{1}{2}\text{AC}$
Hence, we have FE||GH and FE = GH $\text{=}\dfrac{1}{2}\text{AC}$
Similarly HE||GF and HE = GF$\text{=}\dfrac{1}{2}\text{BD}$
Since ABCD is a square, we have AC = BD{Because the diagonals of a square are equal}
Hence we have FE||GH and HE||GF and FE= GH = HE = GF.
Hence EFGH is a rhombus.
Now in the triangle AHE, AH = AE = $\dfrac{a}{2}$, where a is the length of a side of the square.
Hence triangle AHE is an isosceles triangle.
Hence $\angle \text{AHE=}\angle \text{AEH=}x(\text{say)}$
Using angle sum property in triangle AHE, we get
$\begin{align}
  & x+x+90{}^\circ =180{}^\circ \\
 & \Rightarrow 2x=180{}^\circ -90{}^\circ \\
 & \Rightarrow 2x=90{}^\circ \\
 & \Rightarrow x=45{}^\circ \\
\end{align}$
Hence $\angle \text{AHE=45}{}^\circ $.
Similarly, $\angle \text{DHG=45}{}^\circ $.
Now
 \[\begin{align}
  & \angle \text{AHE+}\angle \text{DHG+}\angle \text{GHE=180}{}^\circ \\
 & \Rightarrow \text{45}{}^\circ +\text{45}{}^\circ +\angle \text{GHE}=\text{180}{}^\circ \\
 & \Rightarrow \angle \text{GHE}=\text{90}{}^\circ \\
\end{align}\]
Hence EFGH is a square.

Note: [1] A common mistake done by students is that after showing all the sides to be equal they think that the parallelogram is a square which is not correct. For a parallelogram to be square it should have all sides equal and all angles right.
[2] We can also solve the question as follows

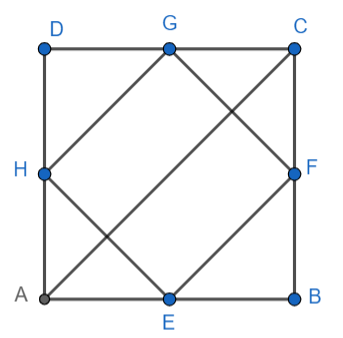
Consider triangles AEH and BEF, we have
AE = BE(Because E is the midpoint of AB)
AH = BF(Both are half the length of the side of the square ABCD)
$\angle HAE=\angle FBE$(Both angles are right angles)
Hence, we have
$\Delta HAE\cong \Delta FBE$(By SAS congruence criterion)
Hence, we have HE = FE.
Similarly, we have HE = GH = GF.
Hence, we have HE = GH = GF = FE.
Also, we have
AH = HE(Both are half the length of a side of the square ABCD)
Hence, we have
$\angle AHE=\angle AEH$
But, we have
$\begin{align}
  & \angle AHE+\angle AEH+\angle HAE=180{}^\circ \\
 & \Rightarrow 2\angle HEA+90{}^\circ =180{}^\circ \\
 & \Rightarrow \angle HEA=45{}^\circ \\
\end{align}$
Similarly, we have
$\angle FEB=45{}^\circ $
Now, we have
$\begin{align}
  & \angle HEA+\angle FEH+\angle FEB=180{}^\circ \\
 & \Rightarrow 45{}^\circ +\angle FEH+45{}^\circ =180{}^\circ \\
 & \Rightarrow \angle FEH=90{}^\circ \\
\end{align}$
Similarly, we have
$\angle EHG=\angle HGE=\angle GFE=90{}^\circ $
Hence, EFGH is a square.
Q.E.D