Question

ABCD is a rhombus such that $\angle ACB = 50^\circ $, find $\angle ADB$.
A) $50^\circ $
B) $40^\circ $
C) $60^\circ $
D) $30^\circ $

Answer 1

Hint: The rhombus has opposite sides equal and parallel. Also it has perpendicular diagonals. Since the opposite sides are parallel, we get pairs of alternate angles. Using these and the sum of angles of a triangle we get the required angle.

Formula used:
The sum of angles of a triangle is $180^\circ $.

Complete step-by-step answer:
Given a rhombus $ABCD$ with $\angle ACB = 50^\circ $.
We are asked to find $\angle ADB$.
Consider the figure.

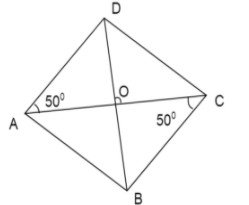
Here $AC,BD$ are the diagonals of the rhombus.
We know that the diagonals of a rhombus are perpendicular to each other.
This gives, $\angle AOB = \angle BOC = \angle COD = \angle DOA = 90^\circ $
Also we have the sides of the rhombus are equal and opposite sides are parallel.
So, $AB\parallel CD$.
Now, the diagonal $AC$ can be considered as a transversal cutting these lines.
This makes $\angle ACB$ and $\angle CAD$ alternate angles and so they are equal.
We get, $\angle ACB = \angle CAD = 50^\circ $
Now consider $\vartriangle AOD$.
We have, $\angle A = 50^\circ $ and $\angle O = 90^\circ $.
We know that the sum of angles of a triangle is $180^\circ $.
So we have, $\angle A + \angle O + \angle D = 180^\circ $
Substituting we get,
$50^\circ + 90^\circ + \angle D = 180^\circ $
Simplifying we get,
$140^\circ + \angle D = 180^\circ $
$ \Rightarrow \angle D = 180^\circ - 140^\circ = 40^\circ $
So we get $\angle ADB = 40^\circ $.
Therefore the answer is option B.

Additional information:
The rhombus is a parallelogram with all sides equal. The diagonals of a rhombus are perpendicular bisectors to each other.


Note: This question can be solved in another way as well. Consider the triangle $\vartriangle BOC$. We know $\angle C$ and $\angle O$. So we can calculate $\angle B$, that is $\angle CBO$. Now we can see $\angle CBO$ and $\angle ADB$ are alternate and are equal. Thus we can find the angle.