Question

\[{\text{ABCD}}\] is a rhombus and \[{\text{P}}\], \[{\text{Q}}\], \[{\text{R}}\]and \[{\text{S}}\] are the midpoints of sides \[{\text{AB}}\], \[{\text{BC}}\], \[{\text{CD}}\] and \[{\text{DA}}\] respectively. Show that quadrilateral \[{\text{PQRS}}\] is a rectangle.

Answer 1

Hint: Here we will use the property of parallelogram and rectangle which states that if opposite sides of a quadrilateral are parallel and equal then it is a parallelogram and if opposite sides of a quadrilateral are parallel and equal with all angles \[{\text{9}}{{\text{0}}^0}\] then it will be a rectangle.

Step-By-Step answer:
Step 1: First of all, by drawing a diagram as per the given information in the question we get:

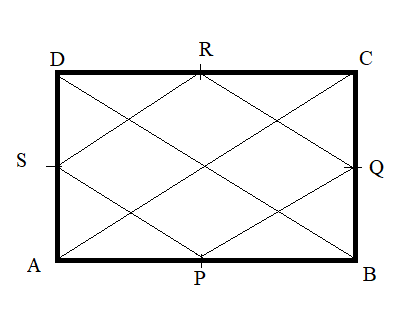
\[{\text{ABCD}}\] is a rhombus and
\[{\text{P}}\], \[{\text{Q}}\], \[{\text{R}}\]and \[{\text{S}}\] are the midpoints of sides \[{\text{AB}}\], \[{\text{BC}}\], \[{\text{CD}}\] and \[{\text{DA}}\]. \[{\text{BD}}\] and \[{\text{AC}}\] are the respective diagonals.
Step 2: Now, as we know that, any line joining by two mid-points will be parallel to its opposite side as shown below:
\[{\text{RQ}}\]is formed by joining the midpoints \[{\text{R}}\]and \[{\text{Q}}\] , so we can say that \[{\text{RQ}}\parallel {\text{BD}}\] and \[{\text{RQ = }}\dfrac{1}{2}{\text{BD}}\]……………… (1)
Similarly, \[{\text{PS}}\]is formed by joining the midpoints \[{\text{P}}\]and \[{\text{S}}\] , so we can say that \[{\text{PS}}\parallel {\text{BD}}\] and \[{\text{PS = }}\dfrac{1}{2}{\text{BD}}\]……………… (2)
By comparing the equation (1) and (2), we get:


\[ \Rightarrow {\text{RQ = PS}}\] also \[{\text{RQ}}\parallel {\text{PS}}\]
Similarly, we can prove it for the lines \[{\text{RS}}\] and \[{\text{PQ}}\]. So, we will get \[{\text{RS = PQ}}\] also \[{\text{RS}}\parallel {\text{PQ}}\]
Now, because \[{\text{PQRS}}\], the opposite sides are equal and parallel then we can say that it is a parallelogram.
Step 3: Now for proving \[{\text{PQRS}}\] is a rectangle, we need to prove that it's one angle is a right angle.
We know that
\[{\text{ABCD}}\] is a rhombus whose all sides are equal, so we can write as below:
\[{\text{AB = BC}}\]
By taking half on both the side of the above expression we get:
\[ \Rightarrow \dfrac{1}{2}{\text{AB = }}\dfrac{1}{2}{\text{BC}}\]
By substituting the value of
\[\dfrac{1}{2}{\text{AB = PB}}\] and\[\dfrac{1}{2}{\text{BC = BQ}}\] in the above expression we get:
 \[ \Rightarrow {\text{PB = BQ}}\]
Now, in a triangle
\[{\text{BPQ}}\], \[{\text{PB = BQ}}\], so their opposite angles will also be equal as shown below:
\[ \Rightarrow \angle {\text{QPB = }}\angle {\text{PQB}}\] …………………………. (3)
Now in \[\Delta {\text{APS}}\] and \[\Delta {\text{CQR}}\], we can write the expressions as below:
\[ \Rightarrow {\text{AB = BC}}\] (sides of a rhombus are equal)
Taking half on both the sides of the above expression we get:
\[ \Rightarrow \dfrac{1}{2}{\text{AB = }}\dfrac{1}{2}{\text{BC}}\]
By substituting the value of
\[\dfrac{1}{2}{\text{AB = AP}}\] and\[\dfrac{1}{2}{\text{BC = CQ}}\] in the above expression we get:

\[ \Rightarrow {\text{AP = CQ}}\]
Similarly, we can write \[{\text{AS = CR}}\] because \[\dfrac{1}{2}{\text{AD = }}\dfrac{1}{2}{\text{CD}}\].
Also, we have
\[{\text{RQ = PS}}\], because the opposite sides of a parallelogram are equal.
So, by using SSS (side-side-side) congruence property, we can say that:
\[ \Rightarrow \Delta {\text{APS}} \cong \Delta {\text{CQR}}\]
So, by using the property of a congruent triangle their corresponding angles will be equal. So we can write as below:
\[ \Rightarrow \angle {\text{SPA = }}\angle {\text{CQR}}\] ………………….. (4)
Step 4: Now we know that the sum of angles in any line will always equal \[{180^0}\]. So, for the line
\[{\text{AB}}\] we can write the equation as below:
\[ \Rightarrow \angle {\text{SPA + }}\angle {\text{SPQ}} + \angle {\text{QPB = 18}}{{\text{0}}^0}\] ……………………….. (5)
Similarly, for line \[{\text{BC}}\], we can write the equation as below:
\[ \Rightarrow \angle {\text{PQB + }}\angle {\text{PQR}} + \angle {\text{CQR = 18}}{{\text{0}}^0}\]
Now, by comparing the above equation with the equations (3) and (4), we get:
\[ \Rightarrow \angle {\text{QPB + }}\angle {\text{PQR}} + \angle {\text{SPA = 18}}{{\text{0}}^0}\] ……………………. (6)
By comparing the equation (5) and (6), we can write the equation as below:
\[ \Rightarrow \angle {\text{QPB + }}\angle {\text{PQR}} + \angle {\text{SPA = }}\angle {\text{SPA + }}\angle {\text{SPQ}} + \angle {\text{QPB}}\]
BY eliminating the same terms from both sides of the above equation we get:
\[ \Rightarrow \angle {\text{PQR = }}\angle {\text{SPQ}}\] ………………….. (7)
Step 5: Now in a parallelogram
\[{\text{PQRS}}\], \[{\text{PS}}\parallel {\text{QR}}\], because these are opposite sides of a parallelogram and \[{\text{PQ}}\] is a transversal so, we can write the equation as below:
 \[ \Rightarrow \angle {\text{PQR + }}\angle {\text{SPQ = 18}}{{\text{0}}^0}\] (\[\because \] interior angles)
But we know that \[\angle {\text{PQR = }}\angle {\text{SPQ}}\] (equation (7)), by substituting this value in the above equation we get:
\[ \Rightarrow \angle {\text{SPQ + }}\angle {\text{SPQ = 18}}{{\text{0}}^0}\]
By adding into the LHS side of the above equation we get:
\[ \Rightarrow 2\angle {\text{SPQ = 18}}{{\text{0}}^0}\]
Bringing \[2\] into the LHS side of the above equation and dividing it we get:
\[ \Rightarrow \angle {\text{SPQ = 9}}{{\text{0}}^0}\]
So, we can say that \[{\text{PQRS}}\] is a rectangle.
 Hence proved that \[{\text{PQRS}}\] is a rectangle.

Note: Students should remember some basic properties of the quadrilateral. Some of them are mentioned below:
> A quadrilateral having opposite sides equal with all angles as right angle then it is called a Rectangle.
> A quadrilateral having all sides equal with all angles as right angle then it is called as Square.
> A quadrilateral having opposite sides equal and parallel then it is called a parallelogram.