Question

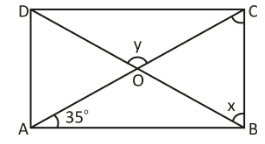
ABCD is a rectangle. Find the values of x and y. If $ \angle OAB = 35^\circ $

Answer 1

Hint: Here we are going to use the properties of the rectangle which states that the diagonals bisect each other and they have the same length. Also, use the properties that vertically opposite angles are equal.

Complete step-by-step answer:
From the given figure and by the properties of the rectangle that the diagonals are equal and they bisect at the point O.
First consider triangle $ \Delta AOB, $
 $ AO = OB $
(Equal diagonals are bisected equally)
From the property – base angles are equal.
 $ \therefore \angle OAB = \angle OBA = 35^\circ $ ..... (i)
We know that sum of all three angles in the triangle is equal to $ 180^\circ $
Therefore, in $ \Delta AOB, $
 $ \angle AOB + \angle OAB + \angle OBA = 180^\circ $
Place values from the equation (i) in the above equation –
 $ \angle AOB + 35^\circ + 35^\circ = 180^\circ $
Simplify the above equation –
 $ \angle AOB + 70^\circ = 180^\circ $
When the term is moved from one side to another, sign is also changed. Positive term changes to negative and vice-versa.
Make the required angle the subject –
 $
  \angle AOB = 180^\circ - 70^\circ \\
  \angle AOB = 110^\circ \;
  $
Observe the given figure, to find that the vertically opposite angles are equal.
Given that $ \angle DOC = y $
 $ \Rightarrow \angle DOC = \angle AOB $
The above relation implies that –
 $ \Rightarrow \angle AOB = \angle DOC = 110^\circ $
Observe the figure once again,
We find that $ \angle ABC = 90^\circ $
Now, consider $ \Delta OBC $
Given that –
\[
  \angle OBC = x^\circ \\
  \angle OBC = \angle ABC - \angle OBA
\]
Place the known values in the above equation –
 $ \Rightarrow \angle OBC = 90^\circ - 35^\circ $
Simplify the above equation –
\[ \Rightarrow \angle OBC = 55^\circ \]
Hence, the required answer is –
 $ x^\circ = 55^\circ $ and $ y^\circ = 110^\circ $
So, the correct answer is “ $ x^\circ = 55^\circ $ and $ y^\circ = 110^\circ $ ”.

Note: A rectangle is the quadrilateral. Each interior angle in the rectangle is equal to $ 90^\circ $ and the sum of all the four angles is equal to $ 360^\circ $ . Also, remember that if the diagonals bisect each other at right angles, then the rectangle is called the square.