Question

ABCD is a rectangle (Figure 11.31) in which \[\overline {DP} \] and \[\overline {BQ} \] are perpendiculars from D and B respectively on diagonal\[\overline {AC} \]. Show that

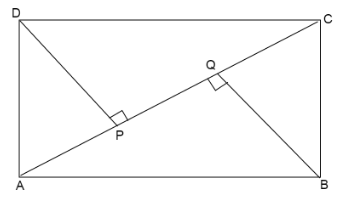
(i) \[\vartriangle ADP \cong \vartriangle CBQ\]
(ii) \[\angle ADP = \angle CBQ\]
(iii) \[\overline {DP} = \overline {BQ} \]

Answer 1

Hint: We prove the congruence in two triangles using AAS congruence rule. Use the definition of alternate interior angles and sides of the rectangle to find pairs of equal sides and angles. After proving congruence, use the CPCT theorem to prove other two parts.
* AAS congruence rule states that the two angles and non-included angle of one triangle is equal to corresponding two angles and non-included side of another triangle.

Complete step-by-step answer:
We are given a rectangle ABCD
Since, ABCD is a rectangle, so opposite sides are parallel and equal to each other.
\[ \Rightarrow AD\parallel BC,AD = BC\](As they are opposite sides of rectangle)...............… (1)
 As AD and BC are set of parallel lines and AC acts as a transversal cutting the parallel lines, the alternate interior angles formed are \[\angle PAD,\angle QCB\]
\[ \Rightarrow \angle PAD = \angle QCB\]………………. (2)

(i) \[\vartriangle ADP \cong \vartriangle CBQ\]
In \[\vartriangle ADP,\vartriangle CBQ\]
\[\angle PAD = \angle QCB\] {From equation (2)}
\[\angle DPA = \angle BQC\]{As they both are perpendiculars to AC}
\[AD = BC\] {From equation (1)}
So, by AAs congruence rule, \[\vartriangle ADP \cong \vartriangle CBQ\]
(ii) \[\angle ADP = \angle CBQ\]
Since, \[\vartriangle ADP \cong \vartriangle CBQ\]
Using the CPCT theorem, the corresponding parts of two triangles are equal.
\[ \Rightarrow \angle ADP = \angle CBQ\] {As they are corresponding angles of congruent triangle}
(iii) \[\overline {DP} = \overline {BQ} \]
Since, \[\vartriangle ADP \cong \vartriangle CBQ\]
Using the CPCT theorem, the corresponding parts of two triangles are equal.
\[ \Rightarrow \overline {DP} = \overline {BQ} \] {As they are corresponding sides of congruent triangle}

Note: * CPCT theorem: CPCT stands for corresponding parts of congruent triangles. Theorem states that when two triangles are congruent, we can write the corresponding parts of two triangles equal.
* Rectangle is a quadrilateral that has the opposite pair of sides parallel and equal to each other. Also, all interior angles of the rectangle are right angles.
* Alternate interior angles are the set of angles that are formed on the alternate sides of a transversal that cuts a pair of parallel lines.