Question

ABCD is a quadrilateral, state whether AB+BC+CD+DA>AC+BD holds true or not?

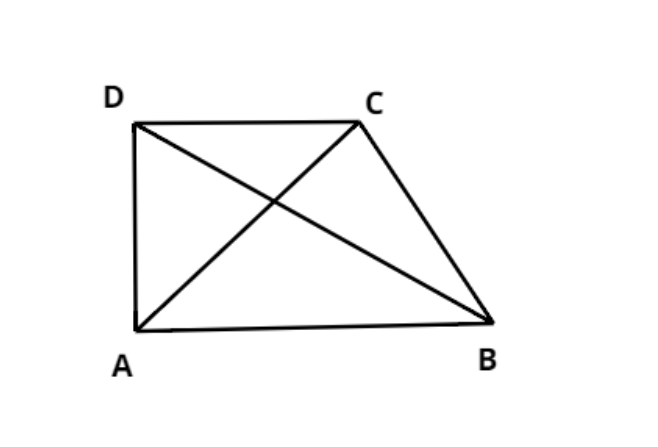
Answer 1

Hint: In this question it is given that ABCD is a quadrilateral, now the diagonals are dividing the quadrilateral into separate triangles, as this is clear from the figure. So use the property of a triangle that the sum of two sides in it will always be greater than the third side.

Complete step-by-step answer:
As we know that in any triangle the sum of two sides is always greater than the third side.
Therefore in triangle ABC we have,
$ \Rightarrow AB + BC > AC$ ……………………………. (1)
Now in triangle ADC we have,
$ \Rightarrow AD + DC > AC$…………………………… (2)
Now in triangle BDC we have,
$ \Rightarrow BC + CD > BD$…………………………… (3)
And in triangle BAD we have,
$ \Rightarrow BA + AD > BD$…………………………… (4)
Now add all this equation we have,
\[ \Rightarrow AB + BC + AD + DC + BC + CD + BA + AD > AC + AC + BD + BD\]
Now simplify the above equation we have,
\[ \Rightarrow 2\left( {AB + BC + CD + DA} \right) > 2\left( {AC + BD} \right)\]
Now divide by 2 throughout we have,
\[ \Rightarrow \left( {AB + BC + CD + DA} \right) > \left( {AC + BD} \right)\]
Therefore in a quadrilateral \[\left( {AB + BC + CD + DA} \right) > \left( {AC + BD} \right)\].
Hence it holds true.
So this is the required answer.

Note: Whenever we face such types of problems the key concept is simply to have a good understanding of the diagrammatic representation provided in the question as it helps in understanding the basic geometry involved in the figure. Some basic properties of triangle few of which have been mentioned while performing the solution always helps in getting on the right track to get the answer for such a problem statement.