Question

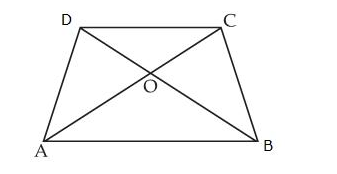
ABCD is a quadrilateral.
Is\[AB + BC + CD + DA > AC + BD?\]

Answer 1

Hint: The quadrilateral is a shape that consists of four vertices, four sides and two diagonals. It also consists of 4 sides and the sum of the angles of a quadrilateral is \[360^\circ \]. When we draw a diagonal, then we can observe the triangles.

Complete step-by-step answer:
The vertices of the quadrilateral are A, B, C and D.
The sides of the quadrilateral are AB, BC, CD and DA.
The diagonals of the quadrilateral are AC and BD.
We know that the statement, the two sides of a triangle is always greater than the third side, so according to this statement,
Now considering the \[\Delta ABC\],
In \[\Delta ABC\], the sum of the sides of the AB and BC is greater than the side AC, it can be written as
\[\Rightarrow AB + BC > AC\]……………..(i)
Now considering the triangle BCD,
In \[\Delta BCD\], the sum of the sides of the BC and DC is greater than the side BD, it can be written as
\[\Rightarrow BC + DC > BD\]……………(ii)
Now considering the triangle ACD,
In \[\Delta ACD\], the sum of the sides of the AD and DC is greater than the side AC, it can be written as
\[\Rightarrow AD + DC > AC\]……………(iii)
Now considering the triangle ABD,
In \[\Delta ACD\], the sum of the sides of the AB and AD is greater than the side BD, it can be written as
\[\Rightarrow AB + AD > BD\]……………(iv)
So, now adding the whole equations right-side terms with a right side and left side terms with the left side terms as shown
\[\Rightarrow AB + BC + AB + AD + AD + DC + BC + DC > AC + AC + BD + BD\]
Simplifying the above equation,
\[
\Rightarrow 2\left( {AB + BC + AD + DC} \right) > 2\left( {AC + BD} \right)\\
\Rightarrow AB + BC + AD + DC > AC + BD
\]
Therefore, it is found that\[AB + BC + AD + DC > AC + BD\].

Note: We have remembered the statements of a triangle while answering this question because when a diagonal is drawn, the quadrilateral looks like two triangles, we can solve this in terms of triangle point of view.