Question

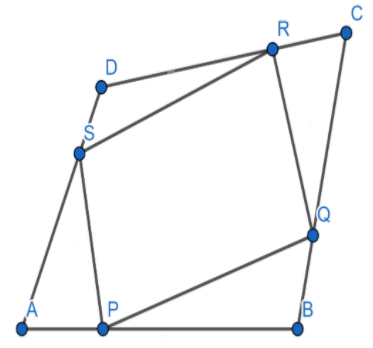
ABCD is a quadrilateral. If P, Q, R, S are the points of trisection of the sides AB, BC, CD, and DA respectively and are adjacent to A and C, then prove that PQRS is a parallelogram.

Answer 1

Hint: Trisection points are the points, which exactly divide the line segment into three equal parts.

In the above line segment A, B, C, D are the points of trisection as they divide the above line segment into three equal parts,
AB: BC: CD = 1:1:1 => AB: BD = 1:2, AC: CD = 2:1

Complete step-by-step solution:
From the question it is given that the points P, Q, R, S are the points of trisection of AB, BC, CD, DA which implies that
AP : PB = 1 : 2, CQ : QB = 1 : 2, CR : RD = 1 : 2, AS : SD = 1 : 2
Now, let us consider the triangle ABC,
From the data derived we have
\[\begin{align}
  & \dfrac{AP}{PB}=\dfrac{1}{2},\dfrac{CQ}{QB}=\dfrac{1}{2} \\
 \Rightarrow &\dfrac{AP}{PB}=\dfrac{CQ}{QB} \\
\end{align}\]
From the converse of Basic proportionality theorem which states that, "In a triangle, if a line segment intersects two sides and divides them in the same ratio, then it will be parallel to the third side".
Since, \[\dfrac{AP}{PB}=\dfrac{CQ}{QB}\], considering the line segment to be SR, from the above theorem we can now say that PQ || AC.
Similarly now let us consider the triangle ADC
From the derived data we now have,
\[\begin{align}
  & \dfrac{CR}{RD}=\dfrac{1}{2},\dfrac{AS}{SD}=\dfrac{1}{2} \\
\Rightarrow & \dfrac{CR}{RD}=\dfrac{AS}{SD} \\
\end{align}\]
From the converse of Basic proportionality theorem which states that, "In a triangle, if a line segment intersects two sides and divides them in the same ratio, then it will be parallel to the third side".
Since, \[\dfrac{CR}{RD}=\dfrac{AS}{SD}\], considering the line segment to be PQ, from the above theorem we can now say that SR|| AC.
Now here we have SR||AC and PQ||AC which implies SR||PQ.
Firstly let us imagine a line segment BD between points B and D.
Now, let us consider the triangle DCB,
From the data derived we have
\[\begin{align}
  & \dfrac{CR}{RD}=\dfrac{1}{2},\dfrac{CQ}{QB}=\dfrac{1}{2} \\
  & \Rightarrow\dfrac{CR}{RD}=\dfrac{CQ}{QB} \\
\end{align}\]
From the converse of Basic proportionality theorem which states that, "In a triangle, if a line segment intersects two sides and divides them in the same ratio, then it will be parallel to the third side".
Since, \[\dfrac{CR}{RD}=\dfrac{CQ}{QB}\], considering the line segment to be RQ, from the above theorem we can now say that RQ || DB.
Similarly now let us consider the triangle ADB
From the derived data we now have,
\[\begin{align}
  & \dfrac{AP}{PB}=\dfrac{1}{2},\dfrac{AS}{SD}=\dfrac{1}{2} \\
 \Rightarrow &\dfrac{AP}{PB}=\dfrac{AS}{SD} \\
\end{align}\]
From the converse of Basic proportionality theorem which states that, "In a triangle, if a line segment intersects two sides and divides them in the same ratio, then it will be parallel to the third side".
Since, \[\dfrac{AP}{PB}=\dfrac{AS}{SD}\], considering the line segment to be DB, from the above theorem we can now say that PS|| DB.
Now here we have PS||DB and RQ||DB which implies PS||RQ.
PS||RQ and SR || PQ can be said from the above conclusions
Hence, it is proved that the PQRS is a parallelogram

Note: Basic proportionality theorem should be known first to know its converse. Basic proportionality states that "If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio". From this, our converse can be derived.