Question

\[ABCD\] is a quadrilateral. If $ AC $ and $ BD $ bisect each other then \[ABCD\] must be a
A. triangle
B. cylinder
C. parallelogram
D. pyramid

Answer 1

Hint: First we draw a diagram according to the information given in the question. We draw a quadrilateral \[ABCD\] and check for the properties of the quadrilateral. One by one we discuss the properties of triangle, cylinder, and parallelogram and pyramid to reach the correct answer.

Complete step-by-step answer:
First let us draw a quadrilateral\[ABCD\]. $ AC $ and $ BD $ are diagonals of a quadrilateral. $ AC $ and $ BD $ bisect each other.

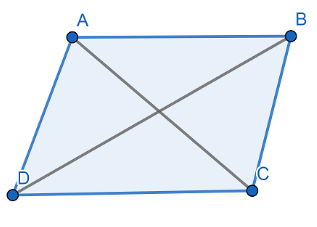
Now, let us discuss the properties of the given options one by one.
Let us start with the triangle-
We know that a triangle is a two dimensional closed shape having three sides and three vertices. Sum of all the interior angles of a triangle is always $ 180{}^\circ $ .

Cylinder- As we know that cylinder is a three dimensional solid shape. A cylinder has two circular bases, which are always parallel and congruent. Cylinder has two circles at the base which are at a particular distance from each other.

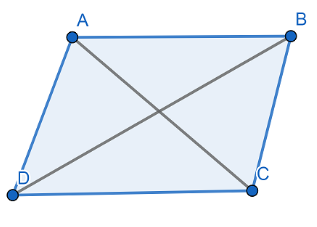
Now, let us discuss the properties of a parallelogram. We know that parallelogram has opposite sides equal and parallel. The diagonal of a parallelogram bisect each other and divides the parallelogram into two congruent triangles.

Now, the last one is the pyramid. A pyramid is a polyhedron with a base that can be any polygon. Pyramid starts with a single point and goes to become wider at the bottom. A pyramid has three or four faces. The vertex in the pyramid is a point where lateral faces meet.
When we discuss the properties of all the shapes given in the option, we reach to the conclusion that option C is the correct answer.
\[ABCD\] is a quadrilateral. If $ AC $ and $ BD $ bisect each other then \[ABCD\] must be a parallelogram.

Note: Alternatively we give the answer to this question directly by eliminating incorrect options. As we know that triangle is not a quadrilateral, so option A is an incorrect answer. Also, as given in the question \[ABCD\] is a quadrilateral and $ AC $ and $ BD $ bisect each other, cylinder and pyramid are not quadrilaterals, so option B and D are incorrect. Option C, parallelogram is the correct answer.