Question

ABCD is a parallelogram, P is a point on side BC such that DP produced meets AB produced at L. Prove that
$
  \left( {\text{i}} \right){\text{ }}\dfrac{{{\text{DP}}}}{{{\text{PL}}}} = \dfrac{{{\text{DC}}}}{{{\text{BL}}}} \\
  \left( {{\text{ii}}} \right){\text{ }}\dfrac{{{\text{DL}}}}{{{\text{DP}}}} = \dfrac{{{\text{AL}}}}{{{\text{DC}}}} \\
 $

Answer 1

Hint: Here, we will proceed by using the property of the parallelogram i.e., Pair of the opposite sides in any parallelogram are always equal and parallel. Here, will also apply Basic Proportionality Theorem i.e., if a line is drawn parallel to one side of a triangle to intersect the other two sides at distinct points then the other two sides are divided in the same ratio.

Complete step-by-step answer:
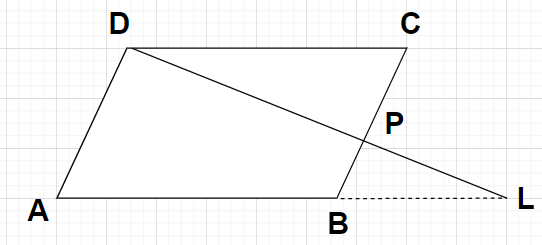
Let us suppose a parallelogram ABCD with sides AB$\parallel $CD and BC$\parallel $AD as shown in the figure.
$\left( {\text{i}} \right)$ To prove: $\dfrac{{{\text{DP}}}}{{{\text{PL}}}} = \dfrac{{{\text{DC}}}}{{{\text{BL}}}}$
As, BC$\parallel $AD and when side BC is divided into two parts i.e., BP and PC then we can write
BP$\parallel $AD and PC$\parallel $AD
According to Basic Proportionality Theorem, if a line is drawn parallel to one side of a triangle to intersect the other two sides at distinct points then the other two sides are divided in the same ratio.
Using the Basic Proportionality Theorem in triangle ALD with BP$\parallel $AD, we can write
$\dfrac{{{\text{BL}}}}{{{\text{AB}}}} = \dfrac{{{\text{PL}}}}{{{\text{DP}}}}{\text{ }} \to {\text{(1)}}$
According to the property of the parallelogram i.e., Pair of the opposite sides in any parallelogram are always equal and parallel.
So, AB = DC [Pair of opposite sides in the parallelogram ABCD]
Using AB = DC in equation (1), we get
$ \Rightarrow \dfrac{{{\text{BL}}}}{{{\text{DC}}}} = \dfrac{{{\text{PL}}}}{{{\text{DP}}}}$
By taking the reciprocal of both sides, we get
$
   \Rightarrow \dfrac{{{\text{DC}}}}{{{\text{BL}}}} = \dfrac{{{\text{DP}}}}{{{\text{PL}}}} \\
   \Rightarrow \dfrac{{{\text{DP}}}}{{{\text{PL}}}} = \dfrac{{{\text{DC}}}}{{{\text{BL}}}} \\
 $
The above equation is the same equation which needs to be proved.

$\left( {{\text{ii}}} \right)$ To prove: $\dfrac{{{\text{DL}}}}{{{\text{DP}}}} = \dfrac{{{\text{AL}}}}{{{\text{DC}}}}$
By equation (1), we have
$\dfrac{{{\text{BL}}}}{{{\text{AB}}}} = \dfrac{{{\text{PL}}}}{{{\text{DP}}}}$
By adding 1 on both sides of the above equation, we get
$
   \Rightarrow \dfrac{{{\text{BL}}}}{{{\text{AB}}}} + 1 = \dfrac{{{\text{PL}}}}{{{\text{DP}}}} + 1 \\
   \Rightarrow \dfrac{{{\text{BL + AB}}}}{{{\text{AB}}}} = \dfrac{{{\text{PL + DP}}}}{{{\text{DP}}}}{\text{ }} \to (2{\text{)}} \\
 $
Clearly from the figure, BL + AB = AL and PL +DP = DL
Using the above equations in equation (2), we get
$ \Rightarrow \dfrac{{{\text{AL}}}}{{{\text{AB}}}} = \dfrac{{{\text{DL}}}}{{{\text{DP}}}}$
Using AB = DC in the above equation, we get
$
   \Rightarrow \dfrac{{{\text{AL}}}}{{{\text{DC}}}} = \dfrac{{{\text{DL}}}}{{{\text{DP}}}} \\
   \Rightarrow \dfrac{{{\text{DL}}}}{{{\text{DP}}}} = \dfrac{{{\text{AL}}}}{{{\text{DC}}}} \\
 $
The above equation is the same equation which needs to be proved.


Note- Converse of Basic Proportionality Theorem also exists in this particular problem i.e., if we would have given that if the ratio in which is a line divides two sides of a triangle are equal, then that line is definitely parallel to the third (or remaining) side of the triangle. Rectangle is a special case of parallelogram in which the interior angles made at each vertex is a right angle.