Question

ABCD is a parallelogram. O is an interior point. If $ar\left( \Delta AOB \right)+ar\left( \Delta COD \right)=43\text{ sq units}$ , then $ar\left( |{{|}^{gm}}ABCD \right)$ is:
(a) 172 sq units
(b) 176 sq units
(c) 86 sq units
(d) 43 sq units

Answer 1

Hint: Start by drawing the representative diagram of the situation given in the figure. We know that the area of the triangle is half of the product of its base and height. So, for the two triangles given in the question the bases AB and CD are parallel, so their heights would be parallel too. Also, the heights pass through point O, so their height is the same line. Now use the sum of the areas of the triangles given in the question to get the height of the parallelogram multiplied by its base, which is the area of the parallelogram.


Complete step-by-step answer:
Let us start the solution to the above question by drawing the representative diagram of the situation given in the figure.

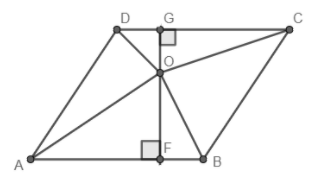
For the two triangles given in the question the bases AB and CD are parallel, so their heights would be parallel too. Also, the heights pass through point O, so their height is the same line.
Now it is given in the question that $ar\left( \Delta AOB \right)+ar\left( \Delta COD \right)=43\text{ sq units}$ and the area of the triangle is equal to $\dfrac{1}{2}\times base\times height$ . For $\Delta AOB$ , AB is the base and OF is the height, while for triangle COD, CO is the base and OG is the height.
 $\dfrac{1}{2}\times AB\times OF+\dfrac{1}{2}\times CD\times OG=43$
Now we know that opposite sides of a parallelogram are equal. So, we can say that AB=CD.
$\dfrac{1}{2}\times AB\times OF+\dfrac{1}{2}\times AB\times OG=43$
$\Rightarrow \dfrac{1}{2}\times AB\left( OF+OG \right)=43$
Now from the figure we can say that OF+OG=FG.
$\dfrac{1}{2}\times AB\times GF=43$
$\Rightarrow AB\times GF=86\text{ sq units}$
Now if we see the figure, AB is the base of the parallelogram and GF is its height as it is perpendicular to both AB and CD and we know that the product of base and height of a parallelogram is equal to its area. So, the $ar\left( |{{|}^{gm}}ABCD \right)$ is equal to 86sq units.
Therefore, the answer to the above question is option (c).

Note:Remember that for a triangle and the parallelogram the base is not fixed and all of its sides can be taken as its base, but once you decide the base, the height is to be chosen accordingly, also it depends on you how wisely you choose the base so that it serves your cause, as we choose in the above question.