Question

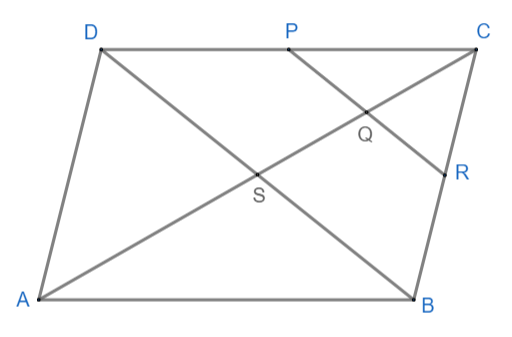
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that $CQ=\dfrac{1}{4}AC$. If PQ produced meets BC at R, prove that R is the midpoint of BC

Answer 1

Hint:
 In this question, we need to prove R as the midpoint of BC. For this, we will first prove Q as the midpoint of CS by using the given condition and using the property of the diagonal of the parallelogram. After that, in $\Delta DCS$ we will use the midpoint theorem. For triangles to prove $PQ\parallel DS$. Using $PQ\parallel DS$ we can say $QR\parallel SB$. So we will use the converse of the midpoint theorem in $\Delta CSB$ to prove R as the midpoint of BC. Theorem and properties are given as:
(I) Diagonals of a parallelogram bisect each other.
(II) Midpoint theorem: the line segment is a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side.
(III) Converse of midpoint theorem: if a line is drawn through the midpoint of one side of a triangle and parallel to the other side, it bisects the third side.

Complete step by step answer:
Here we are given a parallelogram ABCD where P is the midpoint of CD. Also, AC and BD are the two diagonals which meet each other at S. We are given the CQ as $CQ=\dfrac{1}{4}AC$ of AC.
We know that the diagonals of a parallelogram bisect each other. Therefore, CS = AS (BD bisects AC at S).
Since CS becomes half of AC. So, $CS=\dfrac{1}{2}AC\cdots \cdots \cdots \left( 1 \right)$.
Also we are given that, $CQ=\dfrac{1}{4}AC\cdots \cdots \cdots \left( 2 \right)$.
Dividing equation (2) by (1) we get $\dfrac{CQ}{CS}=\dfrac{\dfrac{1}{4}AC}{\dfrac{1}{2}AC}$.
Cancelling AC on the right side we get $\dfrac{CQ}{CS}=\dfrac{\dfrac{1}{4}}{\dfrac{1}{2}}$.
Simplifying the right side we get $\dfrac{CQ}{CS}=\dfrac{1}{2}$.
Taking S to the other side we get $CQ=\dfrac{1}{2}CS$.
Hence Q is the midpoint of CS.
Now in $\Delta CDS$, we see that P is the midpoint of CD and Q is the midpoint of CS. So we can apply the midpoint theorem here.
According to the midpoint theorem, the line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side.
In $\Delta CDS$. P is the midpoint of CD and Q is the midpoint of CS.
Therefore PQ is parallel to the side DS.
Now since QR is just the extension of PQ and SB is the extension of DS, so we can say $QR\parallel SB$.
Therefore, in $\Delta CSB, QR\parallel SB$ and Q is the midpoint of CS.
So we can apply the converse of the midpoint theorem here.
According to the converse of the midpoint theorem, if a line is drawn through the midpoint of one side of a triangle and parallel to the other side, it bisects the third side.
Here $QR\parallel SB$ and Q is the midpoint of CS. So QR bisects BC at R. Hence R is the midpoint of BC.
Hence proved.

Note:
Students should know the statement of the midpoint theorem and its converse. Keep in mind the properties of a parallelogram. Take care while dividing the equation (1) and (2). Note that PQ and QR are parts of line PR. Similarly, DS and SB are parts of DB. So if PQ is parallel to DS then PR is parallel to DB and thus QR is parallel to SB.