Question

ABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively then is GP=PH?
(a) True
(b) False

Answer 1

Hint: To solve this problem, we should know the basics of properties of parallelogram. We should know that the opposite sides of the parallelogram are equal and parallel to each other. Along with that we will use the property that E and F are the mid-points of AB and CD respectively to get the answer to the above question.

Complete step by step answer:
To explain the solution, we will refer to the below figure of the quadrilateral.

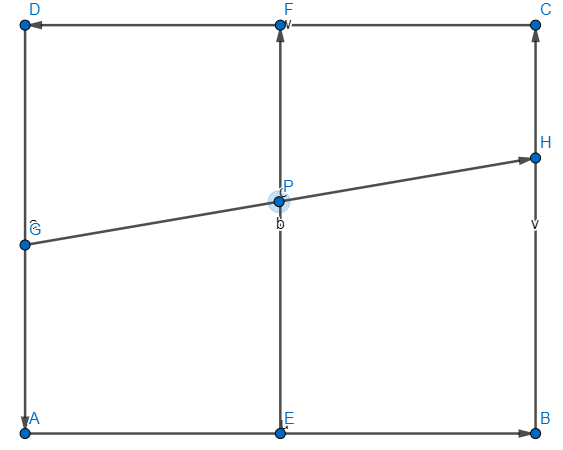
Since E and F are midpoints AB and CD respectively.
Thus, we have, 2AE = 2BE = AB and 2CF = 2DF = ​CD
We also know that AB=CD.
Thus, we have, 2BE = 2​CF = AB = CD.
So, BE = CF.
Also, BE || CF (since, AB || CD; here || indicates that two line segments are parallel to each other)
Thus, we can conclude that BEFC is a parallelogram. (since, BE = CF, BE || CF in the quadrilateral BEFC)
Thus, we have
BC || EF and BE=PH --(1)
Now, from these results, we can say that
AD∥EF (Since, AD || BC because ABCD is a parallelogram, further, BC || EF, thus, AD || BC || EF)
Thus, AEFD is a parallelogram (AE = FD and AD || EF).
But, E is the midpoint of AB. So, we have,
AE=BE -- (2)
Now, also, we have AD || BC || EF and GH is the transversal, we have,
$\dfrac{AE}{EB}=\dfrac{CF}{DF}=\dfrac{GP}{PH}=1$ (Since, AE = BE)
Thus, we have, GP = PH.
Hence, the correct answer is (a) True.

Note: To prove the geometrical results, we always start with the given properties by listing them and then begin to solve the problem. For example, in this problem, we start by using the information of ABCD being a parallelogram and special information of E and F being the mid-points of AB and CD. This way we will eventually arrive at the required property to prove.