Question

ABCD is a parallelogram, as shown in the figure. If AB=2AD and P is mid-point of AB, the \[\angle CPD\]=
A.\[{90^ \circ }\]
B.\[{60^ \circ }\]
C.\[{45^ \circ }\]
D.\[{135^ \circ }\]

Answer 1

Hint: Parallelogram is a simple quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and also opposite angles of a parallelogram are equal.

Complete step-by-step answer:
In this question, it is given P is the midpoint; therefore, AP will be half of the side AB and given AB=2AD; hence side AD will be equal to AP, by using angle opposite to equal side property say opposite sides are equal and find the angle APD then repeat this for triangle PBC to find the angle CPB and by using straight-line angle find angle CPD.
In the given parallelogram AB=2AD and P is the midpoint of AB.
Now draw line PE starting from point P and parallel to side AB

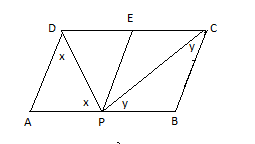
In triangle APD,
AP=PD [Since angle opposite to equal sides are equal]
Let \[\angle APD = \angle ADP = x - - - (i)\]
Since the sum of angles of a triangle are equal to\[{180^ \circ }\], therefore in the triangle APD
\[
  \angle APD + \angle ADP + \angle PAD = 180 \\
  \angle PAD = 180 - \angle APD - \angle ADP \\
  \angle PAD = 180 - x - x \\
  \angle PAD = 180 - 2x - - - (ii) \\
 \]
Now for the triangle BPC,
BP=PC [Since angle opposite to equal sides are equal]
Let \[\angle BPC = \angle PCB = y - - - (iii)\]
Using the sum of internal angle theorem
\[
  \angle BPC + \angle PCB + \angle PBC = 180 \\
  \angle PBC = 180 - \angle BPC - \angle PCB \\
  \angle PBC = 180 - y - y \\
  \angle PBC = 180 - 2y - - - (iv) \\
 \]
Since the sum of adjacent angles in a parallelogram are\[{180^ \circ }\] so
\[\angle PAD + \angle PBC = 180\]
Now add equation (ii) and (iv), we get
\[
  180 - 2x + 180 - 2y = 180 \\
  360 - 2x - 2y = 180 \\
  2x + 2y = 360 - 180 \\
  2\left( {x + y} \right) = 180 \\
  \therefore x + y = 90 \\
 \]
Since APB forms a straight line hence, angle P will be equal to 180,
\[
  \angle P = 180 \\
  \angle APD + \angle CPD + \angle CPB = 180 \\
  \angle CPD + x + y = 180 \\
  \angle CPD = 180 - \left( {x + y} \right) \\
  \angle CPD = 180 - 90 \\
   = {90^ \circ } \\
 \]
Therefore \[\angle CPD = {90^ \circ }\]
So, the correct answer is “Option A”.

Note: Students must note that if the opposite sides of a quadrilateral are not equal, then the given shape is not a parallelogram. At the same time, we cannot say with confirmation that the quadrilaterals with the equal and parallel sides are a parallelogram.