Question

ABCD is a parallelogram and AP and CQ are the perpendiculars from the vertices A and C on the diagonal BD. Show that,
\[\left( i \right)\Delta APB\cong \Delta CQD\]
\[\left( ii \right)AP=CQ\]

Answer 1

Hint: We are given a parallelogram and we have two perpendiculars drawn from the two vertexes. To show \[\Delta APB\cong \Delta CQD\] we will first use that the opposite sides of the parallelogram are equal then we use that as sides are parallel, so alternate interior pairs of angles are equal. With this, using the AAS congruency rule, we claim that our triangle is congruent. AAS means Angle – Angle Side Congruence Rule and for AP = CQ, they will be equal as they are the point of the congruent triangle.

Complete step by step answer:
We are given that ABCD is a parallelogram where AP and CQ are perpendicular to BD. We are asked to show that the triangle APB and triangle CQD are congruent.

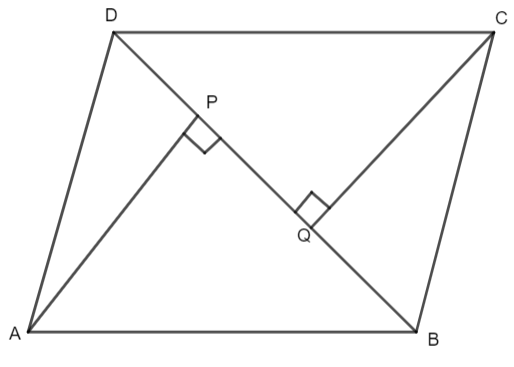
We know that the properties of a parallelogram which tells us that the opposite pair of the sides of the parallelogram are always equal in the length. So, from the figure, we have that AB is the opposite to CD. Hence, we have,
\[AB=CD.....\left( i \right)\]
(As opposite sides are equal)
Now, we also know that along with being equal opposite sides are parallel as well. As AB is opposite to CD, so, AB||CD.
Now, AB||CD and DB will act as transversal (a line which passes through the two parallel). So, as we know in a parallel line, the pair of the alternate interior are always parallel. So, we can see that for AB||CD and DB as transversal, we get,
\[\angle CDB=\angle ABD.....\left( ii \right)\]
Now, we claim that triangle APB and triangle CQD are congruent. So, in triangle APB and triangle CQD we have,
\[\angle APB=\angle CQD={{90}^{\circ }}\left[ \text{Given} \right]\]
\[\angle ABP=\angle CDQ\left[ \text{As }\angle ABD=\angle CDB \right]\]
\[AB=CD\left[ \text{Using (i)} \right]\]
So by the congruence rule AAS, that is Angle – Angle Side, we get,
\[\Delta APB\cong \Delta CQD\]
Hence, we have proved that \[\Delta APB\cong \Delta CQD.\]
(ii) AP = CQ
Now, we have to show that AP = CQ. We know that when the two triangles are congruent, then its corresponding parts are always equal. As we have got that, \[\Delta APB\cong \Delta CQD\] so its corresponding part must be equal. So from here, we get, AP = CQ.
Hence, we get, AP = CQ.

Note: Remember that congruence means that items are identical twins, if we proved that they are congruent then each part of these triangles will be equal. CPCT is the short form which is always used which means the corresponding parts of the congruent triangle. Once, we have proved that two triangles are congruent, then by CPCT, the remaining parts are always equal to each other.