Question

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD. Show that \[AP = CQ\].

Answer 1

Hint: In the given question, we have been given that there is a parallelogram ABCD. On the diagonal BD of the parallelogram ABCD, there are perpendiculars AP and CQ from vertices A and C. We have to show that the length of the given perpendiculars is equal. To show that, we are first going to draw a figure representing the parallelogram. Then, we are going to consider the two triangles containing the perpendiculars and prove that they are congruent. Then we are going to use c.p.c.t. to show that the perpendiculars are equal.

Complete step-by-step answer:
For solving the question, we are first going to draw the figure.

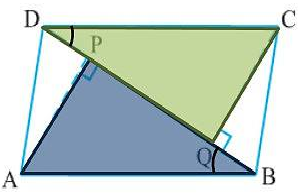
It has been given that \[AP\] and \[CQ\] are perpendicular. Hence, \[\angle DQC = 90^\circ \] and \[\angle APB = 90^\circ \], or
\[\angle DQC = \angle APB\] …(i)
Now, \[DC||AB\] (opposite sides of a parallelogram are parallel)
and, \[BD\] is a transversal.
So, \[\angle CDQ = \angle ABP\] (alternate interior angles) …(ii)
Now, let us consider \[\Delta DQC\] and \[\Delta APB\].
\[\angle DQC = \angle APB\] (from (i))
\[\angle CDQ = \angle ABP\] (from (ii))
\[AB = CD\] (opposite sides of a parallelogram are equal)
Hence, by \[AAS\] congruence rule,
\[\;\Delta DQC \cong \Delta APB\]
Thus, \[AP = CQ\] (by c.p.c.t.)
Hence, proved.

Note: To solve the questions involving proving something in the given statement, we consider the two things being asked about. Then we pair up the combinations of the triangles and take the pair which looks symmetric. Then we prove the triangles to be congruent and then using the similar approach, as did in the question, we prove the equality of the two asked things.