
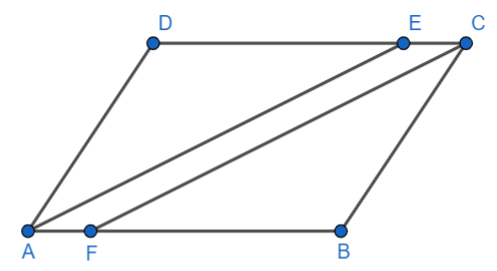
ABCD is a parallelogram, and AE and CF bisect $\angle A$ and $\angle C$ respectively. Prove that $AE\parallel FC$.

Answer
609.3k+ views
Hint: In this given question, we can use the concept of transversal on two lines in order to solve it and get the required proof. As we know in the case of a transversal the corresponding angles are equal and also alternate interior angles are equal. So, here we can prove that $\angle EAF=\angle CFB$. As these are equal corresponding angles, the two line segments, AE and FC, are parallel.
Complete step-by-step answer:
In this given question, it is provided that ABCD is a parallelogram in which AE and CF bisect $\angle A$ and $\angle C$ respectively and we are asked to prove that $AE\parallel FC$.
We are going to use the concept of transversal to two lines to prove the asked condition.
In order to prove $AE\parallel FC$, it is sufficient to prove that any pair of the corresponding angles are equal as parallel lines have equal corresponding angles.
The proof is as follows:
We know that the opposite angles of a parallelogram are equal.
So, $\angle A=\angle C$
$\Rightarrow \dfrac{1}{2}\angle A=\dfrac{1}{2}\angle C$
$\Rightarrow \angle EAF=\angle ECF............(1.1)$ (As AE and CF bisect $\angle A$ and $\angle C$ respectively as given in the question)
Now, we know that alternate interior angles in the case of a transversal on two lines are also equal.
So, $\angle ECF=\angle CFB..............(1.2)$
From equation 1.1 and 1.2, we get
$\begin{align}
& \angle EAF=\angle ECF=\angle CFB \\
& \Rightarrow \angle EAF=\angle CFB...............(1.3) \\
\end{align}$
Now, $\angle EAF\text{ }and\text{ }\angle CFB$ are corresponding angles of transversal AB on AE and FC. Also from equation 1.3, we get that $\angle EAF=\angle CFB$.
Therefore, we get a pair of equal corresponding angles on AE and FC.
Hence, it is proved that $ AE \ parallel FC $, as the condition is satisfied correctly.
Note: In equation (1.1), we should be careful to state that AE and CF bisect the angles $\angle A$ and angle $\angle C$ as it is mentioned in the question and does not follow from any other law of parallelogram.
Complete step-by-step answer:
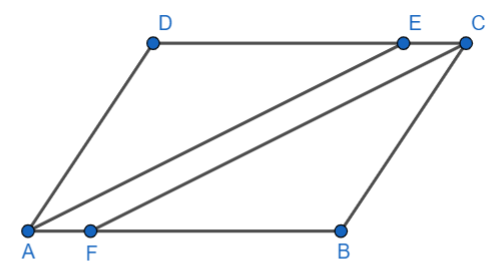
In this given question, it is provided that ABCD is a parallelogram in which AE and CF bisect $\angle A$ and $\angle C$ respectively and we are asked to prove that $AE\parallel FC$.

We are going to use the concept of transversal to two lines to prove the asked condition.
In order to prove $AE\parallel FC$, it is sufficient to prove that any pair of the corresponding angles are equal as parallel lines have equal corresponding angles.
The proof is as follows:
We know that the opposite angles of a parallelogram are equal.
So, $\angle A=\angle C$
$\Rightarrow \dfrac{1}{2}\angle A=\dfrac{1}{2}\angle C$
$\Rightarrow \angle EAF=\angle ECF............(1.1)$ (As AE and CF bisect $\angle A$ and $\angle C$ respectively as given in the question)
Now, we know that alternate interior angles in the case of a transversal on two lines are also equal.
So, $\angle ECF=\angle CFB..............(1.2)$
From equation 1.1 and 1.2, we get
$\begin{align}
& \angle EAF=\angle ECF=\angle CFB \\
& \Rightarrow \angle EAF=\angle CFB...............(1.3) \\
\end{align}$
Now, $\angle EAF\text{ }and\text{ }\angle CFB$ are corresponding angles of transversal AB on AE and FC. Also from equation 1.3, we get that $\angle EAF=\angle CFB$.
Therefore, we get a pair of equal corresponding angles on AE and FC.
Hence, it is proved that $ AE \ parallel FC $, as the condition is satisfied correctly.
Note: In equation (1.1), we should be careful to state that AE and CF bisect the angles $\angle A$ and angle $\angle C$ as it is mentioned in the question and does not follow from any other law of parallelogram.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




