Question

ABCD is a cyclic quadrilateral whose diagonals intersect at point E. If $\angle DBC={{70}^{\circ }}$, $\angle BAC$ is ${{30}^{\circ }}$, find $\angle BCD$. Further, if $AB=BC$, find $\angle ECD$?

Answer 1

Hint: First of all draw the figure of ABCD quadrilateral inside a circle then mark the angles given in the problem then to find the required angles we are going to use the property of cyclic quadrilateral which is the sum of opposite angles of cyclic quadrilateral is ${{180}^{\circ }}$ and we will also use the property that angles on the same segment are equal. As it is given that $AB=BC$ so we will use the property that angles opposite to equal sides are equal.

Complete step-by-step answer:
In the below diagram, we have shown quadrilateral ABCD in a circle with O as centre of the circle and the diagonals intersect at point E. We have also shown $\angle DBC={{70}^{\circ }}$, $\angle BAC$ is ${{30}^{\circ }}$.
 

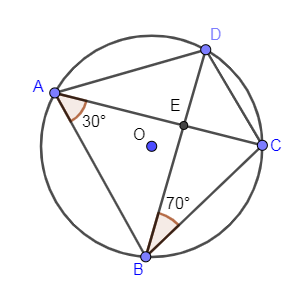
In the above diagram, $\angle DBC=\angle CAD$ because these angles lie on the same segment AB so we know that angles lying on the same segment are equal. As $\angle DBC={{70}^{\circ }}$ so $\angle CAD$ is also equal to ${{70}^{\circ }}$.
$\angle DBC=\angle CAD={{70}^{\circ }}$
In the below diagram, we have modified the above diagram by adding $\angle CAD$ as ${{70}^{\circ }}$.

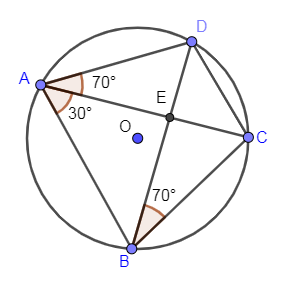
Now, measurement of $\angle BAD$ is equal to sum of $\angle BAC\And \angle CAD$.
$\angle BAD=\angle BAC+\angle CAD$
Substituting $\angle BAC={{30}^{\circ }}$ and $\angle CAD={{70}^{\circ }}$ in the above equation we get,
$\begin{align}
  & \angle BAD={{30}^{\circ }}+{{70}^{\circ }} \\
 & \Rightarrow \angle BAD={{100}^{\circ }} \\
\end{align}$
As ABCD is a cyclic quadrilateral so it is this quadrilateral property that the sum of opposite angles of the quadrilateral is ${{180}^{\circ }}$.
Applying this property in the above diagram, sum of angle BAD and angle BCD is ${{180}^{\circ }}$.
$\angle BAD+\angle BCD={{180}^{\circ }}$
Substituting $\angle BAD={{100}^{\circ }}$ in the above equation we get,
${{100}^{\circ }}+\angle BCD={{180}^{\circ }}$
Subtracting ${{100}^{\circ }}$ on both the sides of the above equation we get,
$\begin{align}
  & \angle BCD={{180}^{\circ }}-{{100}^{\circ }} \\
 & \Rightarrow \angle BCD={{80}^{\circ }} \\
\end{align}$
Hence, we have found the value of $\angle BCD$ as ${{80}^{\circ }}$.
We have shown this angle in the below figure,
 

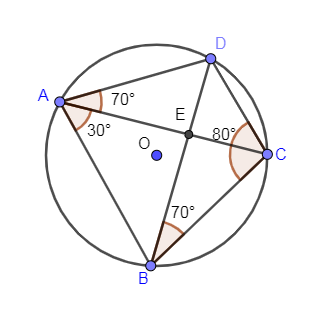
It is also given that $AB=BC$ so we know the property that angles opposite to equal sides are equal. Therefore, angles opposite to sides AB and BC are equal.
Angle opposite to side AB is $\angle BCA$ and angle opposite to side BC is $\angle BAC$. Equating both these angles we get,
$\angle BAC=\angle BCA={{30}^{\circ }}$
Now, the sum of $\angle BCE\And \angle ECD$ is equal to $\angle BCD$.
$\angle BCE+\angle ECD=\angle BCD$
$\angle BCE$ is same as $\angle BCA$ which we have calculated above as ${{30}^{\circ }}$ and $\angle BCD$ as ${{80}^{\circ }}$ so substituting these values in the above equation we get,
$\begin{align}
  & {{30}^{\circ }}+\angle ECD={{80}^{\circ }} \\
 & \Rightarrow \angle ECD={{80}^{\circ }}-{{30}^{\circ }} \\
 & \Rightarrow \angle ECD={{50}^{\circ }} \\
\end{align}$
Hence, we have calculated the value of $\angle ECD={{50}^{\circ }}$.

Note: This question demands a good knowledge of cyclic quadrilateral, properties of angles on the same segment and knowledge of basic geometry that includes angles opposite to equal sides are equal. Deficit with these concepts lead to the failure of solving this problem.
One more thing, you might think how do I know which geometry concepts are required. This problem can be rectified when you proceed with the question using the properties of cyclic quadrilateral that opposite angles sum are ${{180}^{\circ }}$ then using this property will automatically lead you to use the geometry properties that we have discussed above.