Question

ABCD (in order) is a rectangle with AB=CD= $ \dfrac{{12}}{5} $ and BC=DA=5. We take a point P on AD such that the value of $ \angle BPC = 90^\circ $ . Calculate the value of (BP+PC)
A) 5
B) 6
C) 7
D) 8

Answer 1

Hint: In this problem firstly, we will put light on a very basic yet very important topic of Mathematics. We will use the Pythagoras theorem to solve the above-given problem. Pythagoras Theorem – Pythagoras Theorem, also referred to as Pythagorean theorem, states that in a right-angled triangle, the square of the length of the hypotenuse matches the sum of the squares of the respective length of the other two sides.
Formula - $ c = \sqrt {{a^2} + {b^2}} $ (where c is the hypotenuse and a and b are the other sides in a right-angled triangle)

Complete step by step answer:
Now let’s Solve our query –

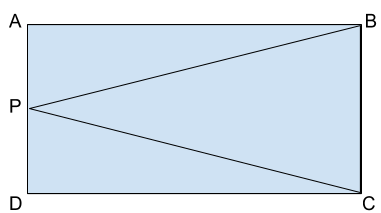
Taking ABP as right-angled triangle, in which $ \angle PAB = 90^\circ $ ,
Now applying Pythagoras theorem,
 $ {(BP)^2} = {(AP)^2} + {(AB)^2} $
 $ \Rightarrow {(BP)^2} = {(AP)^2} + {\left( {\dfrac{{12}}{5}} \right)^2} $
Taking AP as $ x $ , we get
 $ \Rightarrow {\left( {BP} \right)^2} = \left( {\dfrac{{144}}{{25}}} \right) + {x^2} $ -----equation (1)
Taking PDC as right-angled triangle, in which $ \angle PDC = 90^\circ $ ,
Now applying Pythagoras theorem,
 $ {(PC)^2} = {(PD)^2} + {(DC)^2} $
We have given $ DC = \left( {\dfrac{{12}}{5}} \right) $ , and also we have taken $ AP = x $ then $ PD = (5 - x) $ (since, given BC=DA=5 )
 $ \Rightarrow {(PC)^2} = {(5 - x)^2} + {\left( {\dfrac{{12}}{5}} \right)^2} $
 $ \Rightarrow {(PC)^2} = {(5 - x)^2} + \left( {\dfrac{{144}}{{25}}} \right) $ ------ equation (2)
Now,
BP and CP are two non-hypotenuse sides of the right-angled triangle BPC.
So, By Pythagoras theorem in the right-angled triangle, in which $ \angle BPC = 90^\circ $ ,
 $ {(BP)^2} + {\left( {PC} \right)^2} = B{C^2} $
Now putting the values from the equation (1) and the equation (2) and it is also given in the question that BC=DA=5,
 $ \left( {\dfrac{{144}}{{25}} + {x^2}} \right) + \left( {{{\left( {5 - x} \right)}^2} + \dfrac{{144}}{{25}}} \right) = 25 $
 $ \Rightarrow \left( {\dfrac{{144}}{{25}} + {x^2} + 25 - {x^2} - 10x + \dfrac{{144}}{{25}}} \right) = 25 $
 $ \Rightarrow \left( {\dfrac{{144}}{{25}} + {x^2}} \right) + \left( {25 + {x^2} - 10x + \dfrac{{144}}{{25}}} \right) = 25 $
 $ \Rightarrow \left( {2{x^2} + 25 - 10x + \dfrac{{288}}{{25}}} \right) = 25 $
 $ \Rightarrow \left( {2{x^2} - 10x + \dfrac{{288}}{{25}}} \right) = 0 $
 $ \Rightarrow 50{x^2} - 250x + 288 = 0 $
Solving Quadratic equation,
An Equation of form ax²+bx+c=0, where a, b, and c are coefficients the value of x is calculated by the formula
 $ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $
Here, a=50, b=-250, c=288
Putting these values in the equation,
 $ \Rightarrow x = \dfrac{{ - ( - 250) \pm \sqrt {{{( - 250)}^2} - 4 \times 50 \times 288} }}{{2 \times 50}} $
 $ \Rightarrow x = \dfrac{{250 \pm \sqrt {62500 - 57600} }}{{100}} $
 $ \Rightarrow x = \dfrac{{250 \pm \sqrt {4900} }}{{100}} $
 $ \Rightarrow x = \dfrac{{250 \pm 70}}{{100}} $
 $ \Rightarrow x = \dfrac{{250 + 70}}{{100}} $ and $ x = \dfrac{{250 - 70}}{{100}} $
 $ \Rightarrow x = 3.2 $ and $ x = 1.8 $
Now if we take, AP = 3.2 then PD= (5-3.2) =1.8
So, putting the value in the equation (1), we get
 $ \Rightarrow {\left( {BP} \right)^2} = \left( {\dfrac{{144}}{{25}}} \right) + {(AP)^2} $
 $ \Rightarrow {\left( {BP} \right)^2} = \left( {\dfrac{{144}}{{25}}} \right) + {(3.2)^2} $
 $ \Rightarrow BP = \sqrt {\left( {\dfrac{{144}}{{25}}} \right) + {{(3.2)}^2}} $
 $ \Rightarrow BP = \sqrt {\left( {\dfrac{{144}}{{25}}} \right) + 10.24} $
 $ \Rightarrow BP = \sqrt {16} $
 $ \Rightarrow BP = 4 $

So, Now,
 $ \Rightarrow {(PC)^2} = {(1.8)^2} + {\left( {\dfrac{{12}}{5}} \right)^2} $
 $ \Rightarrow PC = \sqrt {{{(1.8)}^2} + \left( {\dfrac{{144}}{{25}}} \right)} $
 $ \Rightarrow PC = \sqrt {3.24 + \left( {\dfrac{{144}}{{25}}} \right)} $
 $ \Rightarrow PC = \sqrt 9 $
 $ \Rightarrow PC = 3 $
Therefore,
 $ BP + PC = 4 + 3 = 7 $
Hence, option (C) is the correct answer.
Note:
There are two values of x for any equation $ a{x^2} + bx + cx = 0 $ . In this question, we have taken the value of the AP = 3.5 then automatically the value of the PD becomes another value of the x i.e. PD= 1.8. Then BP and PC are determined one by one by putting the values. If we interchange the value for the AP and PD that means if we take AP= 1.8 then the value of the PD will be 3.2. In this case, also the value of the final answer will be the same.