Question

ABC is an isosceles triangle with AC = BC. If \[A{{B}^{2}}=2A{{C}^{2}}\], then the value of \[\angle ACB\] is
A). less than \[{{60}^{\circ }}\]
B). equal to \[{{60}^{\circ }}\]
C). equal to \[{{90}^{\circ }}\]
D). less than \[{{30}^{\circ }}\]

Answer 1

Hint: Use cosine law of triangle to get a relation between all three sides and an angle of the triangle. Put appropriate given information and get the result.

Complete step-by-step solution
Let us assume that \[\angle ACB=\theta \] and represent AB, BC, AC as c, a, b respectively. In the below figure, we have shown an isosceles triangle ABC with sides AB, BC, AC as c, a, b respectively, and \[\angle ACB=\theta \].

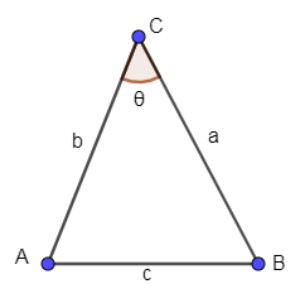
Now it is given that AC = BC. Hence we can write a = b
Again it is given that \[A{{B}^{2}}=2A{{C}^{2}}\]. So, we can write \[{{c}^{2}}=2{{b}^{2}}\]
Now we know from the cosine law that \[{{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\cos \theta \] where every parameter represents standard things.
So using the above equation we get,\[{{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\cos \theta \]
Now as a = b then we get \[{{c}^{2}}={{b}^{2}}+{{b}^{2}}-2{{b}^{2}}\cos \theta \]
\[\Rightarrow {{c}^{2}}=2{{b}^{2}}-2{{b}^{2}}\cos \theta \]
Or we can write \[{{c}^{2}}-2{{b}^{2}}= -2{{b}^{2}}\cos \theta \]
But it is given that \[{{c}^{2}}=2{{b}^{2}}\]. So, \[{{c}^{2}}-2{{b}^{2}}=0\]
Hence, we can write \[2{{b}^{2}}\cos \theta =0\]
As b is non-zero we can cancel it out from both sides and hence we get that \[\cos \theta =0\]
From trigonometry we know that the angle which satisfies the above equation is \[{{90}^{\circ }}\]. Because it is at an angle of a triangle so it has a restricted value.
Hence, the value of \[\angle ACB\] is \[{{90}^{\circ }}\].
Hence, the correct answer to the given question is an option (c) equal to \[{{90}^{\circ }}\]

Note: In the above solution, you might have thought why we have written the solution for \[\cos \theta =0\] as \[{{90}^{\circ }}\], cosine is 0 at the odd multiple of $\dfrac{\pi }{2}$ so $\theta $ can be $\dfrac{3\pi }{2},\dfrac{5\pi }{2}$ and so one. The answer is we know the each of the three angles in a triangle can take value greater than ${{0}^{\circ }}$ and less than $\pi $ and the angles from $\dfrac{3\pi }{2},\dfrac{5\pi }{2}$ and so on are greater than $\pi $ that’s why we have not consider these solutions and only took $\theta =\dfrac{\pi }{2}$.