Question

$ABC$ is an isosceles triangle with $AB = AC$and $AD$ is one of its altitude . State the three pairs of equal parts in $\Delta ADB$ and $\Delta ADC$.

Answer 1

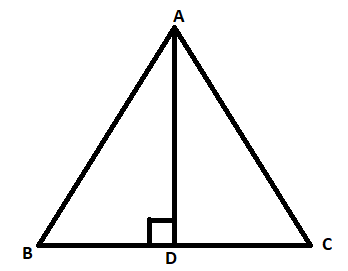
Hint:In this question $ABC$ is an isosceles triangle and we know isosceles triangles are those whose two sides are of equal length. So, draw the diagram with an altitude $AD$ and find the three pairs of equal parts .

Complete step-by-step answer:

Now, we have
$
  AB = AC \\
   \Rightarrow \angle B = \angle C \\
$
As $AD$ is an altitude , hence
$\Delta ADB = \Delta ADC = {90^ \circ }$
Three pairs of equal parts in $\Delta ADB$ and $\Delta ADC$ are-
$
  AB = AC \\
  \angle B = \angle C \\
  \Delta ADB = \Delta ADC \\
 $
As two pairs of angles in $\Delta ADB$ and $\Delta ADC$ are equal, hence third pair will also be equal
$\angle DAB = \angle DAC$
Note: It is advisable for such types of questions to draw the diagram and equalize the sides who are of equal length , in order to solve the question easily . According to the question there is an isosceles triangle whose two sides are of equal measure , So before starting draw a figure of an isosceles triangle with altitude.