Question

ABC is an isosceles triangle right angled at B. Similar triangles ACD and ABE are constructed in sides AC and AB. Find the ratio between the areas of $\Delta ABE$ and $\Delta ACD$ .
\[\begin{align}
  & \left( A \right)2:1 \\
 & \left( B \right)1:1 \\
 & \left( C \right)1:2 \\
 & \left( D \right)none \\
\end{align}\]

Answer 1

Hint: This particular problem requires some basic as well as advanced knowledge of trigonometry, similarity of triangles and geometry. Here we need to know an important thing that, whenever two similar triangles are given in any problem, the ratio of the areas of the two triangles are equal to the ratio of the square of their respective sides. In the main triangle ABC we can easily find out a relation between all the sides of the triangle using the Pythagoras theorem.

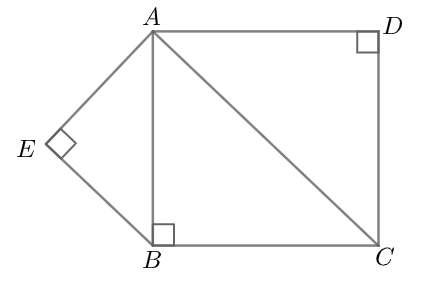
Complete step-by-step solution:
Now we start off with the solution the given problem by writing that, the ratio of the areas of the two triangles \[\Delta ABE\] and \[\Delta ACD\] is given by,
\[\dfrac{\Delta ABE}{\Delta ACD}=\dfrac{A{{B}^{2}}}{A{{C}^{2}}}\]
Now from the original triangle \[\Delta ABC\] we can easily find a relation using the Pythagoras theorem that,
\[A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\]
Now since ABC is an isosceles triangle, we have \[AB=BC\] . Putting this in the above equation we get,
\[A{{C}^{2}}=2A{{B}^{2}}\]
Using this relation in the ratio of the area we get,
\[\begin{align}
  & \dfrac{\Delta ABE}{\Delta ACD}=\dfrac{A{{B}^{2}}}{2A{{B}^{2}}} \\
 & \Rightarrow \dfrac{\Delta ABE}{\Delta ACD}=\dfrac{1}{2} \\
\end{align}\]
Thus, we get the required ratio as \[\dfrac{1}{2}\] . So, option C is the correct answer.

Note: To solve these questions efficiently we need to have a thorough knowledge of geometry, trigonometry and similarities of triangles. We can also solve this particular problem using plain trigonometry, but it would be a lengthy process and is prone to mistakes. This method on the other hand is a much simpler process with less chances of error. We must remember that for any two similar triangles, the ratio of their areas is equal to the ratio of the square of their respective sides.