Question

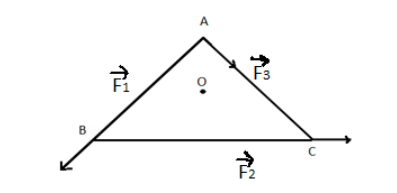
ABC is an equilateral triangle with O as its centre, \[\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \] and \[\overrightarrow {{F_3}} \] represented three forces acting along the sides of $AB,BC$ and $AC$ respectively. If the total torque about O is zero then the magnitude of $\overrightarrow {{F_3}} $ is?
     

A. $\dfrac{{{F_1} + {F_2}}}{2}$
B. $2\left( {{F_1} + {F_2}} \right)$
C. ${F_1} + {F_2}$
D. ${F_1} - {F_2}$

Answer 1

Hint: We can solve this question with the concept of rotational equilibrium in the rotation motion topic. When the body moves or revolves around a fixed axis, this type of motion is called rotational motion. In the pure rotational motion, every particle in the rotating object moves in the circle about the same axis and the radius vectors for all particles make the same angular displacement at the same time.

Complete step-by-step answer:
The dynamics of the rotational motion is much similar to the dynamics of linear or translational. In rotational motion torque is analogous to the force and mass to the inertia. So when the sum of all the external torque acting on the body is zero then the body is called in the rotational equilibrium like the translational equilibrium. When the torque is zero, the object is experiencing zero angular acceleration and either it will not be moving or moving with constant angular velocity.
Torque is defined as it will cause objects to accelerate angularly. An object is in rotational equilibrium when, sum of all the torque is zero : $\sum\limits_{}^{} \tau = 0$.
In the question, ABC is an equilateral triangle with O as its centre, \[\overrightarrow {{F_1}}, \overrightarrow {{F_2}} \] and \[\overrightarrow {{F_3}} \] represented three forces acting along the sides of $AB,BC$ and $AC$ respectively. So after the addition of all the anticlockwise and clockwise torque,
$
  {F_1}d + {F_2}d - {F_3}d = 0 \\
  {F_3} = {F_1} + {F_2} \\
$
Where $d$ is distance from the centre of the triangle. If the total torque about O is zero then the magnitude of $\overrightarrow {{F_3}} $ $ = {F_1} + {F_2}$, so the correct option is option C.

Note: We know that the translational motion and the rotational motion are analogue to each other. For rotational motion it is not necessary that the axis must go through the body it can exist anywhere around the body or in the body.