Question

ABC is a triangle with \[\angle A = {30^ \circ },BC = 10cm\] . The area of the circumcircle of the triangle is
A.\[100\pi \;sqcm\]
B.\[5\;sqcm\]
C.\[25\;sqcm\]
D.\[\dfrac{{100\pi }}{3}\;sqcm\]

Answer 1

Hint: Firstly, construct the diagram with the help of given information. Find the dimensions of the triangle in order to get the value for radius of the circumcircle. Then find the area of the circumcircle using the formula \[\pi {r^2}\]. The circumcircle of a triangle always passes through all the vertices of the triangle.

Complete step-by-step answer:
Construction of diagram as per the given dimensions:
                       

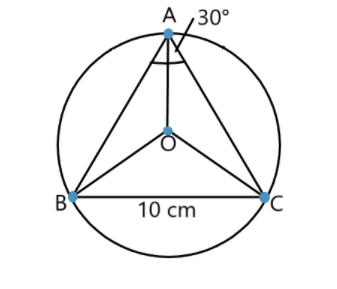
Given that ABC is a triangle and \[\angle A = {30^ \circ },BC = 10cm\] .
We need to find the area of the circumcircle of the triangle.
Let O be the center of the circumcircle of the given triangle.
According to the Inscribed Angle Theorem, we know that:
The centered angle is equal to twice of the opposite angle.
So, \[\angle BOC = 2\angle A\]
Therefore, \[\angle BOC = {60^ \circ }\]
Hence OB and OC are the radii of the circumcircle of the given triangle.
Thus, \[\angle OBC = \angle OCB = {60^ \circ }\]
Therefore, OBC is an equilateral triangle.
The radius of the circle\[ = OB = OC = BC = 10cm\]
Hence the area of the circumcircle of a triangle \[ = \pi {r^2}\]
Since, the radius of the circumcircle of the given triangle is \[10\,cm\].
Therefore, we get the area of the circumcircle of a triangle as:
 \[ = \pi {10^2} = 100\pi \]
Therefore, area of the circumcircle \[ = 100\pi {\text{ sq cm}}\]
Hence, we get the required answer to the question.
So, the correct answer is “Option A”.

Note: Locate accurately which line of the triangle forms the radius of the circumcircle. Keep in mind that the circumcircle of a triangle always passes through all the vertices of the triangle. We should have accuracy in calculations, derivatives and arithmetic in order to be sure of the final answer. We must know that there may be additional information given in the question that is not of use in solving the problem.