Question

ABC is a triangle whose medians intersect each other at point G. If one of its median is AD, then prove that Area $ \left( {\Delta ACD} \right) = 3 \times $ Area $ \left( {\Delta GCD} \right) $ .

Answer 1

Hint: In this problem, we have given that the medians of a triangle ABC intersect each other at point G and one of its median is AD. Triangle is a basic shape of geometry which has three sides and three vertices. In triangle ABC, A,B,C are the vertices of the triangle and AB, BC, CA are the sides of the triangle.
Formula Used: Area of triangle $ = \dfrac{1}{2} \times $ base $ \times $ altitude

Complete step-by-step answer:
In the triangle ABC, G is the centroid of the triangle as, here all the medians of the triangle intersect. Let us draw a rough figure of the triangle ABC and let the medians are D, E and H and the centroid of the triangle is G.

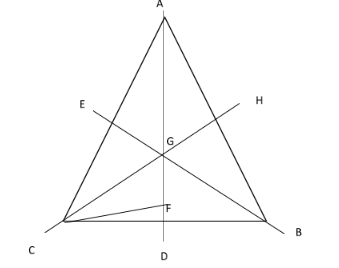
And we drawn an altitude from C on AD at F and we know that, the centroid of triangle divides each triangle in ratio $ 2:1 $ , so we can say that
 $ AG:GD = 2:1 $ or we can also say that $ GD = \dfrac{1}{3}AD $ . Now,
 area of triangle ACD $ = \dfrac{1}{2} \times $ base $ \times $ altitude
 $ = \dfrac{1}{2} \times AD \times CF $
Area of triangle GCD $ = \dfrac{1}{2} \times $ base $ \times $ altitude
 $ = \dfrac{1}{2} \times GD \times CF $
 $ $ Now, we will substitute the value of GD i.e, $ GD = \dfrac{1}{3}AD $ and after substituting it becomes,
 $ = \dfrac{1}{2} \times \dfrac{1}{3}AD \times CF $
Now, we will take the ratio of area of triangle ACD and area of triangle GCD, here we will representing area as ar,
 $ \dfrac{{ar\left( {\Delta ACD} \right)}}{{ar\left( {\Delta GCD} \right)}} = \dfrac{{\dfrac{1}{2} \times AD \times CF}}{{\dfrac{1}{2} \times \dfrac{1}{3}AD \times CF}} $
On further solving we get,
 $ \dfrac{{ar\left( {\Delta ACD} \right)}}{{ar\left( {\Delta GCD} \right)}} = 3 $
It is also written as,
 $ ar\left( {\Delta ACD} \right) = 3 \times ar\left( {\Delta GCD} \right) $
Hence, it is proved.

Note: The median of a triangle divides the triangle into two equal parts and where all the medians of a triangle intersect each other then, that point is known as the centroid, in this problem G is the centroid of the triangle ABC and the centroid of a triangle divides each median of a triangle into ratio of $ 2:1 $ .