Question

AB is a diameter of a circle and AD is a chord. If AB = 26 cm, AD = 24 cm, the distance of AD from the centre of the centre of the circle is
(a) 8 cm
(b) 5 cm
(c) 12 cm
(d) 10 cm

Answer 1

Hint: Here, draw figure using given information in question. Find DB using Pythagoras theorem. Then draw perpendicular from OC to AD, prove two triangles form similar triangles. Using properties of a similar triangle, find the length of perpendicular drawn from O to AD.

Complete step-by-step answer:
Draw figure based on information given in the question

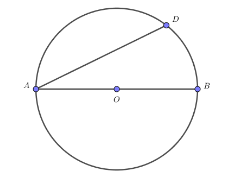
Here AB = 26 cm and AD = 24 cm, O is the centre of the circle.
Now, join DB and draw a perpendicular from O to AD, where perpendicular meets AD at C.
Distance of chord AD from the centre of the circle is OC.

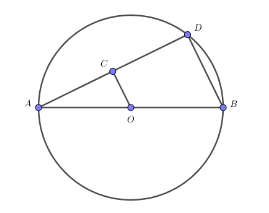
Now, in above figure, ∠ADB = 90° [Angle in semicircle]
Also, ∠ACO = 90° [CO is perpendicular to AD]
In triangle ADB, ∠B = 90°
Then, $ A{D^2} + D{B^2} = A{B^2} $ [Using Pythagoras Theorem]
Putting values of AD and AB,
 $ {(24)^2} + D{B^2} = {(26)^2} $
Rearranging the terms
 $ \Rightarrow D{B^2} = {(26)^2} - {(24)^2} $
 $ \Rightarrow D{B^2} = 676 - 576 = 100 $
 $ \Rightarrow DB = \sqrt {100} = 10 $
Thus, DB = 10 cm.
Now, in triangles ACO and ADB
∠A = ∠A [Common in both triangles]
∠ACO = ∠ADB [Each equal to 90°]
By AA similarity criteria both triangles are similar.
So, $ \dfrac{{AD}}{{AC}} = \dfrac{{AO}}{{AB}} = \dfrac{{OC}}{{DB}} $
[In two triangles corresponding sides are in same proportion]
Consider, $ \dfrac{{AO}}{{AB}} = \dfrac{{OC}}{{DB}} $
 $ \Rightarrow \dfrac{{13}}{{26}} = \dfrac{{OC}}{{10}} $
 $ \Rightarrow OC = \dfrac{{10}}{2} = 5 $
Thus, OC = 5 cm.
So, the correct answer is “OC = 5 cm”.

Note: In these types of questions, first drawn the figure to understand the question geometrically. Always remember the angle of the semicircle is 90°. That is, if we draw a triangle where two vertices are endpoints of diameter of a circle and the third vertex touches the circumference of the circle, then the angle of the third vertex is always 90°. As one angle of the triangle formed is 90°, we can find the unknown side using Pythagoras theorem.